cho △ABC Cân tại A.Trên tia đối BC lấy điểm D, CB lấy điểm E .Sao cho BD=CEa) Cm: △ABD=△ACEb)Cm; △ADE cânc)kẻ BH vuông góc với AD,CK vuông góc với AE,CM:AH=AKd)kéo dài BH cắt CK tại O,CM:△OBC Cân Tại OCM là viết tắt của Chứng minh nha các bạn, với vẽ hình giùm minh nhé ,cảm ơn rất...
Đọc tiếp
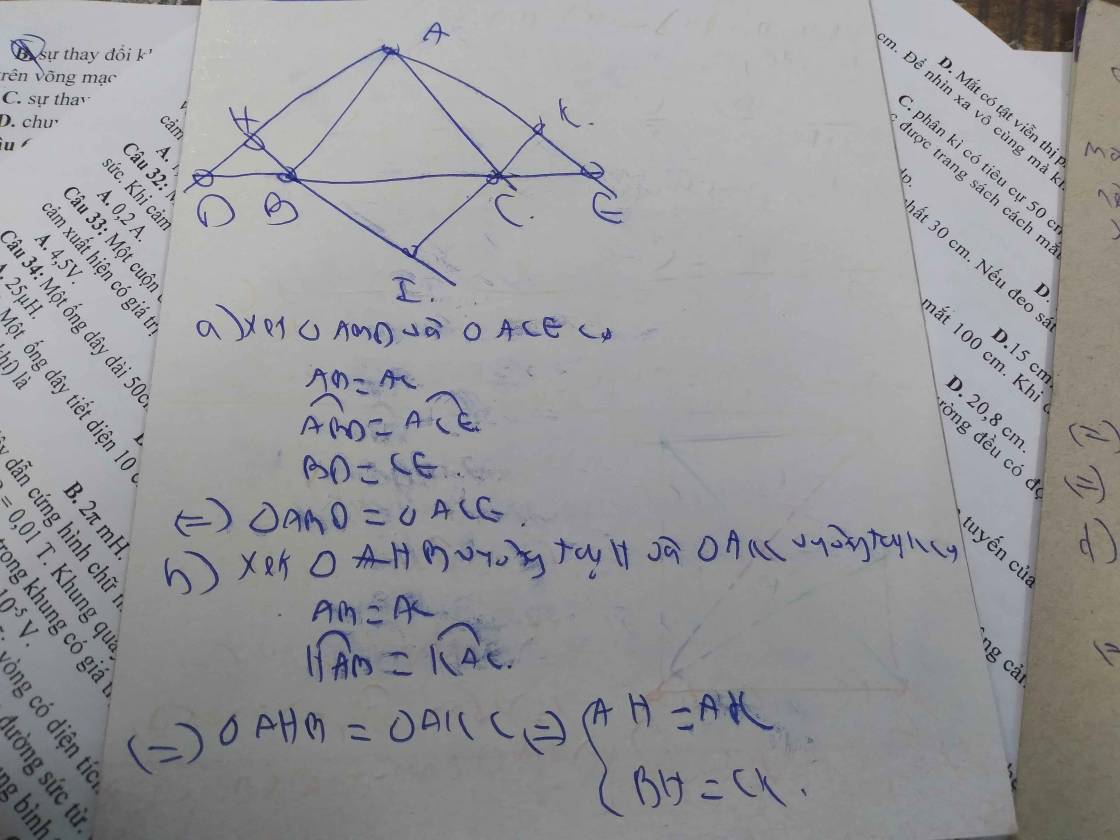
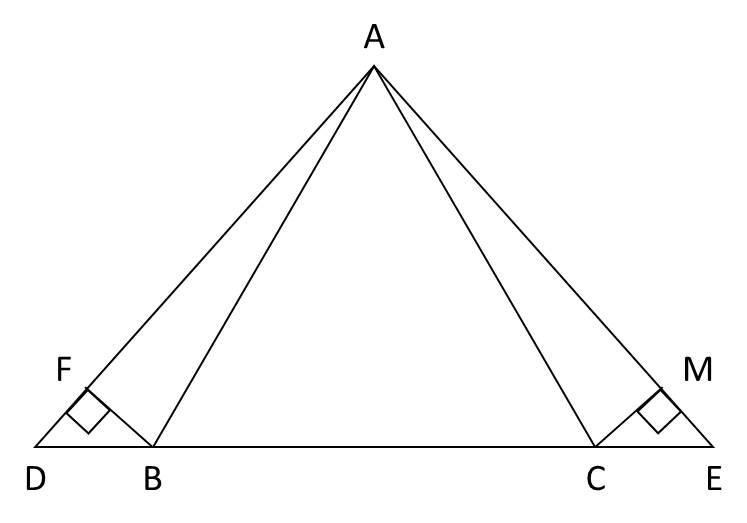
cho △ABC Cân tại A.Trên tia đối BC lấy điểm D, CB lấy điểm E .Sao cho BD=CE
a) Cm: △ABD=△ACE
b)Cm; △ADE cân
c)kẻ BH vuông góc với AD,CK vuông góc với AE,CM:AH=AK
d)kéo dài BH cắt CK tại O,CM:△OBC Cân Tại O
CM là viết tắt của Chứng minh nha các bạn, với vẽ hình giùm minh nhé ,cảm ơn rất nhiều
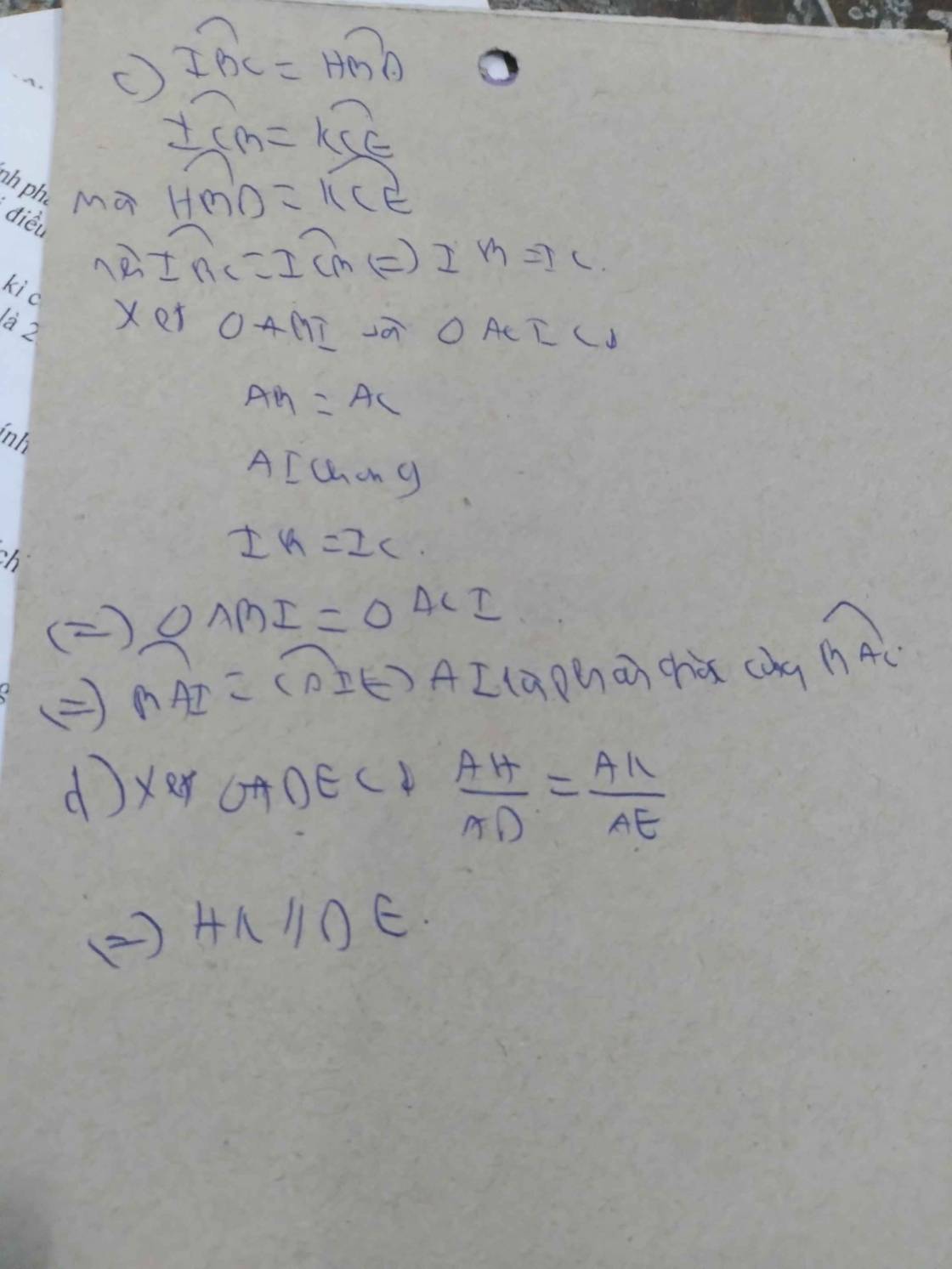
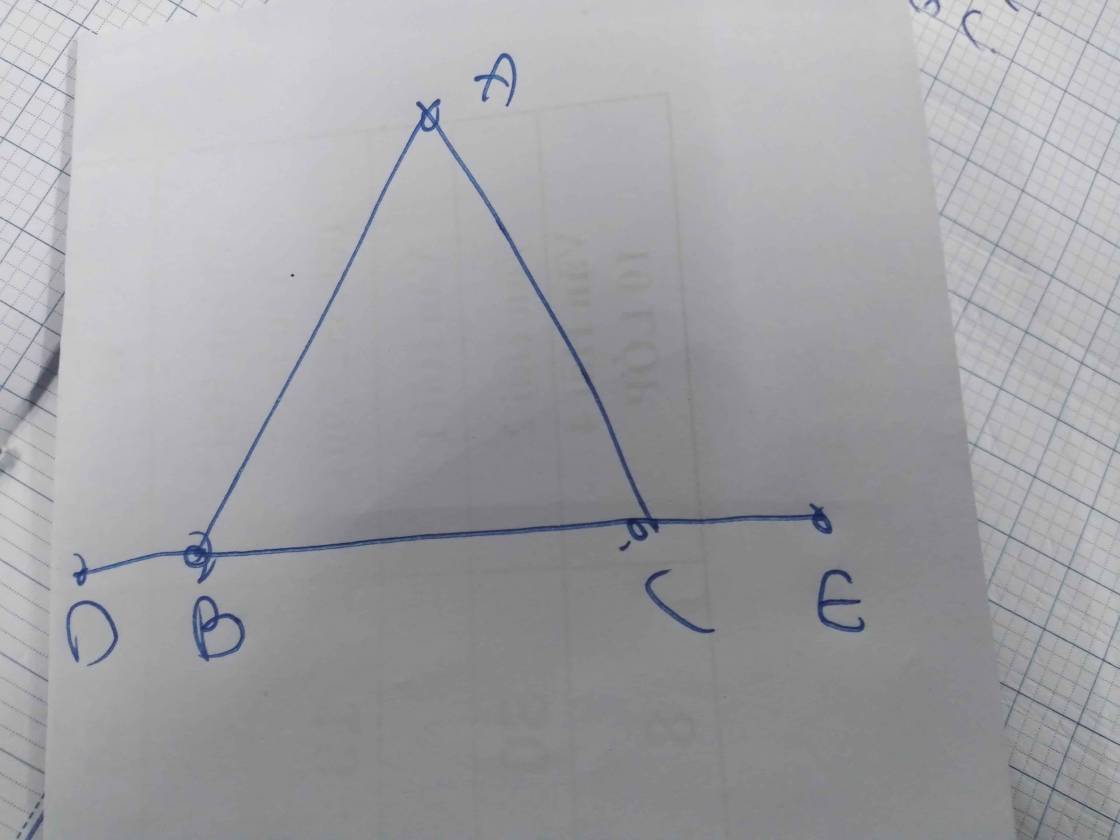
giúp mình với
a) Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACE}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABD}=\widehat{ACE}\)
Xét ΔABD và ΔACE có
AB=AC(ΔBAC cân tại A)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
BD=CE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
b) Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(Hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
c) Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC(ΔBAC cân tại A)
\(\widehat{HAB}=\widehat{KAC}\)(ΔABD=ΔACE)
Do đó: ΔABH=ΔACK(Cạnh huyền-góc nhọn)
Suy ra: AH=AK(Hai cạnh tương ứng)
d) Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE(gt)
BH=CK(ΔABH=ΔACK)
Do đó: ΔHBD=ΔKCE(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)(hai góc tương ứng)
mà \(\widehat{HBD}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCE}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)