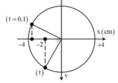
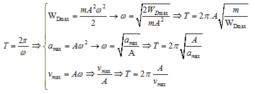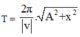Một chất điểm dao động điều hoà với phương trình x = 4cos(10πt - π/6) cm a) Viết biểu thức của vận tốc và gia tốc của chất điểm theo t? b) Tìm li độ, vận tốc, gia tốc của chất điểm tại thời điểm t = 2 s? c) Tại những thời điểm nào li độ của chất điểm bằng 2 cm. d) Tại những thời điểm nào vận tốc của chất điểm bằng 0. e) Tính vận tốc cực đại của chất điểm? f) Tính vận tốc của chất điểm khi có li độ 2 cm.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Phương trình: \(x=2cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
a)Biên độ: \(A=2cm\)
Chu kì: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{5\pi}=0,4s\)
Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{0,4}=2,5Hz\)
Chiều dài quỹ đạo: \(L=2A=2\cdot2=4cm\)
b)Phương trình chất điểm:
Vận tốc: \(v=-\omega Asin\left(\omega t+\varphi\right)=-10\pi sin\left(5\pi t-\dfrac{\pi}{4}\right)\)
Gia tốc: \(a=-\omega^2Acos\left(\omega t+\varphi\right)=-500cos\left(5\pi t-\dfrac{\pi}{4}\right)\)
c)Em thay giá trị \(t=0,2s\) vào từng pt nhé.

a/ \(4A=4.6=24\left(cm\right)\)
\(f=\frac{\omega}{2\pi}=\frac{4\pi}{2\pi}=2\left(Hz\right)\)
\(\varphi_0=\frac{\pi}{6}\left(rad\right)\)
b/ \(v=-\omega A\sin\left(\omega t+\varphi\right)=-4\pi.6.\sin\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=-4.\pi.6.\frac{-1}{2}=12\pi\left(cm/s\right)\)
\(a=-\omega.x=-4\pi.6\cos\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=-4\pi.6.\frac{-\sqrt{3}}{2}=12\sqrt{3}\pi\left(rad/s\right)\)
\(x=6.\cos\left(4\pi.\frac{1}{4}+\frac{\pi}{6}\right)=6.\frac{-\sqrt{3}}{2}=-3\sqrt{3}\left(cm\right)\)
d/ \(v_{max}=\omega A=4\pi.6=24\pi\left(cm/s\right)\)
\(a_{max}=\omega^2A=\left(4\pi\right)^2.6=96\pi^2\left(rad/s\right)\)

Đáp án D
Dùng máy tính bấm nhanh tổng hợp dao động:
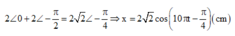
Vận tốc sớm pha π 2 so với li độ nên
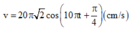
Tại thời điểm t = 8 s
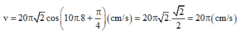

Đáp án C
Tần số góc của dao động 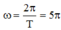
→ Thời điểm t = 0,1s ứng với góc lùi ![]()
Biểu diễn các vị trí tương ứng trên đường tròn, ta thu được:
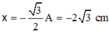
![]()