Cho tam giác ABC. Gọi D,E,F lần lượt là trung điểm của AB,BC,AC.
a) Tam giác ABC và DEF có đồng dạng với nhau không?
b) Tam giác DEF đồng dạng với tam giác ABC theo tỉ số nào?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhh uuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyyoiyygyhiui

Bài 7:
Đặt a=A'B',b=A'C', c=B'C'
Theo đề,ta có: a/6=b/8=c/10
mà cạnh nhỏ nhất trong tam giác A'B'C' là 9cm
nên b/8=c/10=9/6=3/2
=>b=12cm; c=15cm

Tự vẽ hình~
Xét tam giác ABC và tam giác DFE
\(\frac{AB}{EF}=\frac{6}{12}=\frac{1}{2}\)
\(\frac{AC}{FE}=\frac{9}{18}=\frac{1}{2}\)
\(\frac{BC}{DE}=\frac{12}{24}=\frac{1}{2}\)
\(\Rightarrow\frac{AB}{DF}=\frac{AC}{FE}=\frac{BC}{DE}=\frac{1}{2}\)
=>Tam giác ABC đồng đang với tam giác DFE (c.c.c)

Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 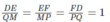
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.

Ta có:
Tam giác ABC dồng dạng tam giác DEF ( gt )
=> ^B = ^E
\(\Rightarrow\dfrac{BC}{EF}=\dfrac{AB}{AC}=k\)
\(\Rightarrow\dfrac{BM}{EN}=\dfrac{BC:2}{EF:2}=\dfrac{BC}{EF}=\dfrac{AB}{DE}=k\)
Xét tam giác ABM và tam giác DEN, có:
^ B = ^E ( cmt )
\(\dfrac{BM}{EN}=\dfrac{AB}{DE}\)
Vậy tam giác ABM đồng dạng tam giác DEN ( c.g.c )
Xét tam giác ACM và tam giác DFN, có:
^C = ^F ( tam giác ABC đồng dạng tam giác DEF )
\(\dfrac{CM}{FN}=\dfrac{AC}{DF}=k\) ( cmt )
Vậy tam giác ACM đồng dạng tam giác DFN ( c.g.c )
\(\Rightarrow\dfrac{AC}{DF}=\dfrac{AM}{DN}\)
Phải đặt k là tỉ số đồng dạng chứ
Có cách khác nè
Do M, N lần lươt là TĐ của BC và EF
\(\Rightarrow MB=MC=\dfrac{1}{2}BC;EN=FN=\dfrac{1}{2}EF\)
Vì △ABC ~ △DEF
\(\Rightarrow\dfrac{BC}{EF}=\dfrac{AB}{DE}\left(2\right)\)
Xét \(\dfrac{MB}{EN}=\dfrac{\dfrac{1}{2}BC}{\dfrac{1}{2}EF}=\dfrac{BC}{EF}\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow...\)
Bạn tự chứng minh được DE =1/2 AC ,EF =1/2 AB và DF =1/2 BC
Do đó: Tam giác ABC đồng dạng với tam giác DEF (c.c.c)
b, Tam giác DEF đồng dạng với tam giác ABC theo tỉ số 2 cạnh tương ứng là DE/AC =2 (hoặc EF/AB,DF/BC thì cũng ra 2)
Chúc bạn học tốt.
Tham khảo qua link này nhé bạn :
https://lazi.vn/edu/exercise/cho-tam-giac-abc-goi-d-e-f-lan-luot-la-trung-diem-cua-ab-bc-ac-a-tam-giac-abc-va-def-co-dong-dang-voi-nhau-khong
Học tốt