Question

[Khưu Hách Nam]

Cho tam giác ABC có \(\widehat{A}=110^o\),M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK=MA.

a) Tính số đo của góc ACK.

b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và AD=AB,AE vuông góc với AC và AE=AC. Chứng minh rằng \(\Delta CAK=\Delta AED.\)

c) Chứng minh rằng MA vuông góc với DE

Các bn giúp mk nha.

Answer 1

[Nguyễn Tất Đạt]

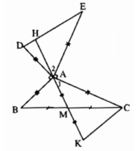
a) \(\Delta\)ABM = \(\Delta\)KCM (c.g.c) => ^ABM = ^KCM (2 góc tương ứng) => AB // CK (2 góc so le trong bằng nhau)

=> ^BAC + ^ACK = 180⁰ (2 góc trong cùng phía) => ^ACK = 180⁰ - 110⁰ = 70⁰

b) \(\Delta\)ABM = \(\Delta\)KCM (cmt) => AB = KC (2 cạnh tương ứng). Mà AB = AD => CK = AD

Ta có: ^BAC + ^BAD + ^CAE + ^DAE = 360⁰ => ^BAC + ^DAE = 180⁰

Mà ^BAC + ^ACK = 180⁰ => ^DAE = ^ACK hay ^DAE = ^KCA

Xét \(\Delta\)CAK và \(\Delta\)AED có: CK=AD; CA=AE; ^KCA = ^DAE => \(\Delta\)CAK = \(\Delta\)AED (đpcm).

c) Tia MA giao DE tại điểm H.

\(\Delta\)CAK = \(\Delta\)AED (cmt) => ^CAK = ^AED (2 góc tương ứng) hay ^CAK = ^AEH

Mà ^CAK + ^HAE = 180⁰ - ^CAE = 90⁰ => ^AEH + ^HAE = 90⁰ => \(\Delta\)AHE vuông tại H

=> AH vuông góc với DE hay MA vuông góc DE (đpcm).