cho dãy (Un) thỏa mãn Un+1 = Un +n(n+1) \(\forall n\ge1.\)
Gọi no là số tự nhiên nhỏ nhất sao cho \(U_{n0}\ge33300\)
Tìm điều kiện của n0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Phương pháp: Dễ thấy u n = u n - 1 + 6 , ∀ n ≥ 2 suy ra dãy số đã cho là cấp số cộng công sai bằng 6.
Vậy ta cần tìm số hạng đầu.
Cách giải: Ta có
log 2 u 5 + log 2 u 9 + 8 = 11
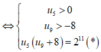
![]()
![]()
V ậ y u 1 = u 5 - 4 . 6 = 8
Do đó:
S n = u 1 + u 2 + . . + u n
= n u 1 + n ( n - 1 ) 2 d
= 3 n 2 + 5 n
⇔ 3 n 2 + 5 n - 32 > 0
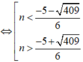
Vậy số tự nhiên n nhỏ nhất thỏa mãn S n ≥ 2 5 là 3.
Không chi biết \(U_1\)bằng bao nhiêu ah.
Cứ thế từ từ thôi
\(U_{n_0}=U_{n_0-1}+\left(n_0-1\right)n_0=U_{n_0-2}+\left(n_0-1\right)n_0+\left(n_0-2\right)\left(n_0-1\right)=...=U_1+\left(n_0-1\right)n_0+...+1.2\)
Làm tiếp ha