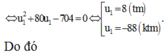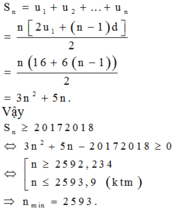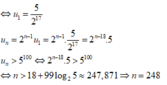Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Đặt t = 2 + log u 1 - 2 log u 10 ≥ 0
⇔ 2 log u 1 - 2 log u 10 = t 2 - 2 ,
khi đó giả thiết trở thành:
log u 1 - 2 log u 10 + 2 + log u 1 - 2 log u 10 = 0
⇔ t 2 + t - 2 = 0
<=> t = 1 hoặc t = -2
⇒ log u 1 - 2 log u 10 = - 1
⇔ log u 1 + 1 = 2 log u 10
⇔ log 10 u 1 = log u 10 2 ⇔ 10 u 1 = u 10 2 ( 1 )
Mà un+1 = 2un => un là cấp số nhân với công bội q = 2
=> u10 = 29 u1 (2)
Từ (1), (2) suy ra
10 u 1 = 9 9 u 1 2 ⇔ 2 18 u 1 2 = 10 u 1 ⇔ u 1 = 10 2 18
⇒ u n = 2 n - 1 . 10 2 18 = 2 n . 10 2 19 .
Do đó u n > 5 100 ⇔ 2 n . 10 2 19 > 5 100
⇔ n > log 2 5 100 . 2 19 10 = - log 2 10 + 100 log 2 5 + 19 ≈ 247 , 87
Vậy giá trị n nhỏ nhất thỏa mãn là n = 248.

Đặt \(log_5\left(x+5\right)=a\Rightarrow x+5=5^a\)
\(\Rightarrow a^2-\left(m+6\right)log_25^a+m^2+9=0\)
\(\Leftrightarrow a^2-a\left(m+6\right)log_25+m^2+9=0\)
\(\Delta=\left(m+6\right)^2.log^2_25-4\left(m^2+9\right)\ge0\)
\(\Leftrightarrow\left(log^2_25-4\right)m^2+\left(12log_2^25\right).m+36\left(log_2^25-1\right)\ge0\)
Bấm máy BPT trên và lấy số nguyên gần nhất ta được \(m\ge-2\Rightarrow\) có \(20+2+1=23\) giá trị nguyên của m

ĐKXĐ: x>0
\(\dfrac{3^2}{3^{log_3x}}=81x\Leftrightarrow\dfrac{9}{x}=81x\Leftrightarrow x^2=\dfrac{1}{9}\Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\left(l\right)\\x=\dfrac{1}{3}\end{matrix}\right.\)
Vậy pt có nghiệm duy nhất \(x=\dfrac{1}{3}\)

thay \(n=5\)vào phương trình trên => \(log_3\left(2u_5-63\right)=2log_4\left(u_5-32\right)=t\) => \(\left\{{}\begin{matrix}2u_5-63=3^t\\u_5-32=2^t\end{matrix}\right.\)
=> \(\left\{{}\begin{matrix}2u_5-63=3^t\\2u_5+32=2.2^t\end{matrix}\right.\)=>\(1+2.2^t=2^t\Leftrightarrow\dfrac{1}{3^t}+2.\left(\dfrac{2}{3}\right)^t=1\)(1)
Vì \(y=\dfrac{1}{3^t}+2.\left(\dfrac{2}{3}\right)^t\) là hàm nghịch biến trên R nên (1) có nghiệm duy nhất t=2 => \(u_5=36\). Thay vào pt ban đầu: \(log_3\left(2.36-63\right)=2log_4\left(u_n-8n+8\right)\)\(\Leftrightarrow u_n=8n-4=4+8\left(n-1\right)\)
=> \(S_n=\dfrac{n\left(8+8\left(n-1\right)\right)}{2}=4n^2\)
=> \(\dfrac{u_n.S_{2n}}{u_{2n}.S_n}=\dfrac{\left(8n-4\right)\left(16n^2\right)}{\left(16n-4\right).4n^2}=\dfrac{4\left(2n-1\right)}{\left(4n-1\right)}< \dfrac{148}{75}\)
=> \(n< 19\)\(\Rightarrow n_{max}=18\)

ĐKXĐ: \(x>0\)
\(\Leftrightarrow log_2^2\left(2x\right)+log_2\left(2x\right)-log_28-9< 0\)
\(\Leftrightarrow log_2^2\left(2x\right)+log_2\left(2x\right)-12< 0\)
\(\Leftrightarrow\left(log_2\left(2x\right)+4\right)\left(log_2\left(2x\right)-3\right)< 0\)
\(\Leftrightarrow-4< log_2\left(2x\right)< 3\)
\(\Leftrightarrow\frac{1}{16}< 2x< 8\Leftrightarrow\frac{1}{32}< x< 4\)