- Tìm x
- x2+x=0
- 2x2-x=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-2018x=0\\ \Leftrightarrow x\left(x-2018\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-2108=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=2018\end{matrix}\right.\)
Vậy `x=0` hoặc `x=2018`
\(2x^2+5x=0\\ \Leftrightarrow x\left(2x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\2x+5=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)
Vậy `x=0` hoặc `x=-5/2`

- Để hàm số đã cho có đạo hàm tại x = 0 khi và chỉ khi:
+ Hàm số liên tục tại x = 0
+ Đạo hàm bên trái và đạo hàm bên phải tại điểm x = 0 bằng nhau.
+) Ta có:
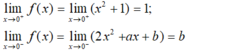
- Do đó, để hàm số liên tục tại x = 0 khi b = 1.
+) Ta có: f(0) = 1.
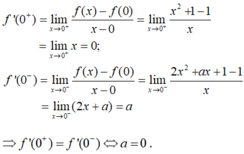
- Vậy a = 0, b = 1 là những giá trị cần tìm.
Chọn C.

Đáp án C.
- Để hàm số đã cho có đạo hàm tại x = 0 khi và chỉ khi:
+ Hàm số liên tục tại x = 0.
+ Đạo hàm bên trái và đạo hàm bên phải tại điểm x = 0 bằng nhau.
+) Ta có:
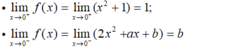
- Do đó, để hàm số liên tục tại x= 0 khi b = 1 .
+) Ta có: f(0) = 1.
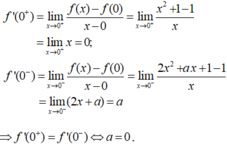
- Vậy a = 0, b = 1 là những giá trị cần tìm.

Chọn B.
- Với x > 0 ta có 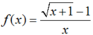 nên hàm số liên tục trên (0; +∞)
nên hàm số liên tục trên (0; +∞)
- Với x < 0 ta có f(x) = 2x2 + 3m + 1 nên hàm số liên tục trên (-∞; 0).
Do đó hàm số liên tục trên R khi và chỉ khi hàm số liên tục tại x = 0
Ta có: f(0) = 3m + 1
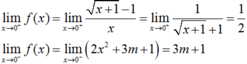
Do đó hàm số liên tục tại 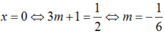 .
.

1.\(\left(x+2\right)\left(2x-3\right)=x^2-4\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3\right)-\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3-x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)
2.\(x^2+3x+2=0\)
\(\Leftrightarrow x^2+x+2x+2=0\)
\(\Leftrightarrow x\left(x+1\right)+2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\end{matrix}\right.\)
3.\(2x^2+5x+3=0\)
\(\Leftrightarrow2x^2+2x+3x+3=0\)
\(\Leftrightarrow2x\left(x+1\right)+3\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(2x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{3}{2}\end{matrix}\right.\)
4.\(x^3+x^2-12x=0\)
\(\Leftrightarrow x\left(x^2+x-12\right)=0\)
\(\Leftrightarrow x\left(x+4\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\\x=3\end{matrix}\right.\)
a: \(\Leftrightarrow\left(x+2\right)\left(2x-3\right)-\left(x+2\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(2x-3-x+2\right)=0\)
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
b: =>(x+1)(x+2)=0
=>x=-1 hoặc x=-2
c: =>(2x+3)(x+1)=0
=>x=-1 hoặc x=-3/2
d: =>x(x+4)(x-3)=0
hay \(x\in\left\{0;-4;3\right\}\)

x - x * 2 + x * 2 - 2 - 3 = 0
x - 2 = 0 + 3
x - 2 = 3
x = 3 + 2
x = 5
X + X x 2 + X x 2 - 2 - 3 = 0
X + X x 2 + X x 2 = 0 + 3 + 2 = 5
X x 1 + X x 2 + X x 2 = 5
X x (1 + 2 + 2) = 5
X x 5 = 5
X = 5 : 5
X = 1

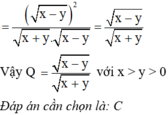
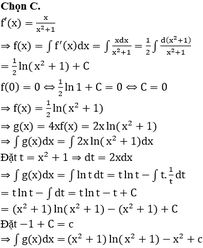
a) \(x^2+x=0\)
\(\Rightarrow x\left(x+1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x+1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-1\end{cases}}\)
Vậy x = 0 hoặc x = -1
b) \(2x^2-x=0\)
\(\Rightarrow x\left(2x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\2x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\2x=1\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{1}{2}\end{cases}}\)
Vậy \(x=0\)hoặc \(x=\frac{1}{2}\)
_Chúc bạn học tốt_
a,x=0;x=-1
b,x=0