
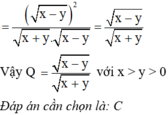
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

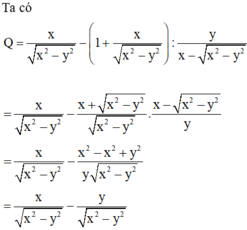
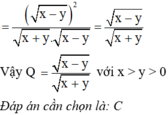

Ta có :
\(\frac{2}{x}-\frac{1}{y}=\frac{1}{2x+y}\Leftrightarrow\frac{2y-x}{xy}=\frac{1}{2x+y}\)
⇔ ( 2y - x ) ( 2x + y ) = xy
⇔ 4xy + 2y2 - 2x2 - xy = xy
⇔ 2y2 - 2x2 = - 2xy
⇔ x2 - y2 = xy
⇔ x4 - 2x2y2 + y4 = x2y2
⇔ x4 + y4 = 3x2y2
Lại có : \(\frac{x^2}{y^2}+\frac{y^2}{x^2}=\frac{x^4+y^4}{x^2y^2}=\frac{3x^2y^2}{x^2y^2}=3\)
Vậy . . . . . . . . .

1) \(x^2+y=y^2+x\Leftrightarrow x^2-y^2-\left(x-y\right)=0\Leftrightarrow\left(x-y\right)\left(x+y-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y=x\\y=1-x\end{cases}}\). Vì x,y là hai số khác nhau nên ta loại trường hợp x = y. Vậy ta có y = x-1.
\(P=\frac{x^2+\left(1-x\right)^2+x\left(1-x\right)}{x\left(1-x\right)-1}=\frac{x^2+x^2-2x+1-x^2+x}{-x^2+x-1}\)
\(=\frac{x^2-x+1}{-\left(x^2-x+1\right)}=-1\)

\(\left\{{}\begin{matrix}x+1=a\\y+1=b\end{matrix}\right.\) \(\Rightarrow a+b=4\)
\(P=\frac{1}{\sqrt{a^2+1}+a}+\frac{1}{\sqrt{b^2+1}+b}=\sqrt{a^2+1}-a+\sqrt{b^2+1}-b\)
\(P=\sqrt{a^2+1}+\sqrt{b^2+1}-4\)
\(P\ge\sqrt{\left(a+b\right)^2+\left(1+1\right)^2}-4=2\sqrt{5}-4\)
\(P_{min}=2\sqrt{5}-4\) khi \(a=b=2\) hay \(x=y=1\)

tự chứng minh x3 +y3 +z3= 3xyz.
Từ x +y +z =0 => \(\hept{\begin{cases}y+z=-x\\x+z=-y\\x+y=-z\end{cases}}\)
Xét: \(\frac{x^2}{y^2+z^2-x^2}\)=\(\frac{x^2}{\left(y+z\right)^2-2yz-x^2}\)=\(\frac{x^2}{x^2-2yz-x^2}\)=\(\frac{x^2}{-2yz}\)
Tương tự ta có \(\frac{y^2}{x^2+z^2-y^2}\)=\(\frac{y^2}{-2xz}\); \(\frac{z^2}{x^2+y^2-z^2}\)=\(\frac{z^2}{-2xy}\)
=> P= \(\frac{x^2}{-2xy}-\frac{y^2}{2xz}-\frac{z^2}{2xy}\)=\(\frac{x^3}{-2xyz}-\frac{y^3}{2xyz}-\frac{z^3}{2xyz}\)=\(\frac{1}{-2xyz}\left(x^3+y^3+z^3\right)\)=\(\frac{3xyz}{-2xyz}=\frac{-3}{2}\)
Tui mới lớp 8 cũng làm đc nhá!!!