Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Trung điểm của CD là M. Tìm giao tuyến của các mặt phẳng sau đây:
a) (SAC) và (SBD) b) (SBM) và (SAC)
c) (SBM) và (SAD) d) (SAM) và (SBC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 10 2023
a: \(M\in\left(BMN\right);M\in SA\subset\left(SAC\right)\)
=>\(M\in\left(BMN\right)\cap\left(SAC\right)\)
\(C\in BN\subset\left(BMN\right);C\in\left(SAC\right)\)
=>\(C\in\left(BMN\right)\cap\left(SAC\right)\)
Do đó: \(CM=\left(BMN\right)\cap\left(SAC\right)\)
b: Xét (BMN) và (SAD) có
BN//AD
\(M\in\left(BMN\right)\cap\left(SAD\right)\)
Do đó: \(\left(BMN\right)\cap\left(SAD\right)=xy\); xy đi qua M và xy//BN//AD
d: Xét (MCD) và (SAB) có
CD//AB
\(M\in\left(MCD\right)\cap\left(SAB\right)\)
Do đó: (MCD) giao (SAB)=ab, ab đi qua M và ab//CD//AB
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 9 2021
Nối BC và AD kéo dài cắt nhau tại F
\(\Rightarrow SF=\left(SBC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối CM kéo dài cắt SD tại G
\(\Rightarrow AG=\left(AMC\right)\cap\left(SAD\right)\)
Trong mp (SCD), nối SM kéo dài cắt CD tại E
\(\Rightarrow AE=\left(SAM\right)\cap\left(ABCD\right)\)
Trong mp (ABCD), nối BE cắt AC tại H
\(\Rightarrow SH=\left(SBM\right)\cap\left(SAC\right)\)
CM
24 tháng 3 2019
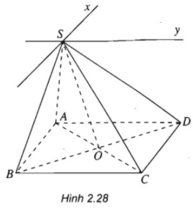
a)
Ta có:
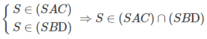
Giả sử:
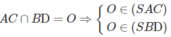
⇒ O ∈ (SAC) ∩ (SBD)
⇒ (SAC) ∩ (SBD) = SO
b) Ta có:
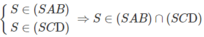
Ta lại có
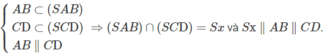
c) Lập luận tương tự câu b) ta có ⇒ (SAD) ∩ (SBC) = Sy và Sy // AD // BC.
a, Gọi \(I=AC\cap BD\)
Mà \(AC\in\left(SAC\right);BD\in\left(SBD\right)\)
\(\Rightarrow I=\left(SAC\right)\cap\left(SBD\right)\)
Lại có \(S=\left(SAC\right)\cap\left(SBD\right)\Rightarrow SI\) là giao tuyến cần tìm.
b, Gọi \(K=AC\cap BM\)
Mà \(AC\in\left(SAC\right);BM\in\left(SBM\right)\)
\(\Rightarrow K=\left(SAC\right)\cap\left(SBM\right)\)
Lại có \(S=\left(SAC\right)\cap\left(SBM\right)\Rightarrow SK\) là giao tuyến cần tìm.
c, Gọi \(N=AD\cap BM\)
Mà \(AD\in\left(SAD\right);BM\in\left(SBM\right)\)
\(\Rightarrow N=\left(SAD\right)\cap\left(SBM\right)\)
Lại có \(S=\left(SAD\right)\cap\left(SBM\right)\Rightarrow SN\) là giao tuyến cần tìm.
d, Gọi \(T=AM\cap BC\)
Mà \(AM\in\left(SAM\right);BC\in\left(BMC\right)\)
\(\Rightarrow T=\left(SAM\right)\cap\left(SBC\right)\)
Lại có \(S=\left(SAM\right)\cap\left(SBC\right)\Rightarrow ST\) là giao tuyến cần tìm.