Câu 1: Cho tam giác ABC vuông tại A có AB>AC, M là một điểm thuộc cạnh AC (M khác A và M khác C). Gọi (O) là đường tròn tân O đường kính MC. Đường thẳng BC cắt đường tròn (O) tai điểm thứ hai D. AD cắt (O) tai điểm thứ hai S.
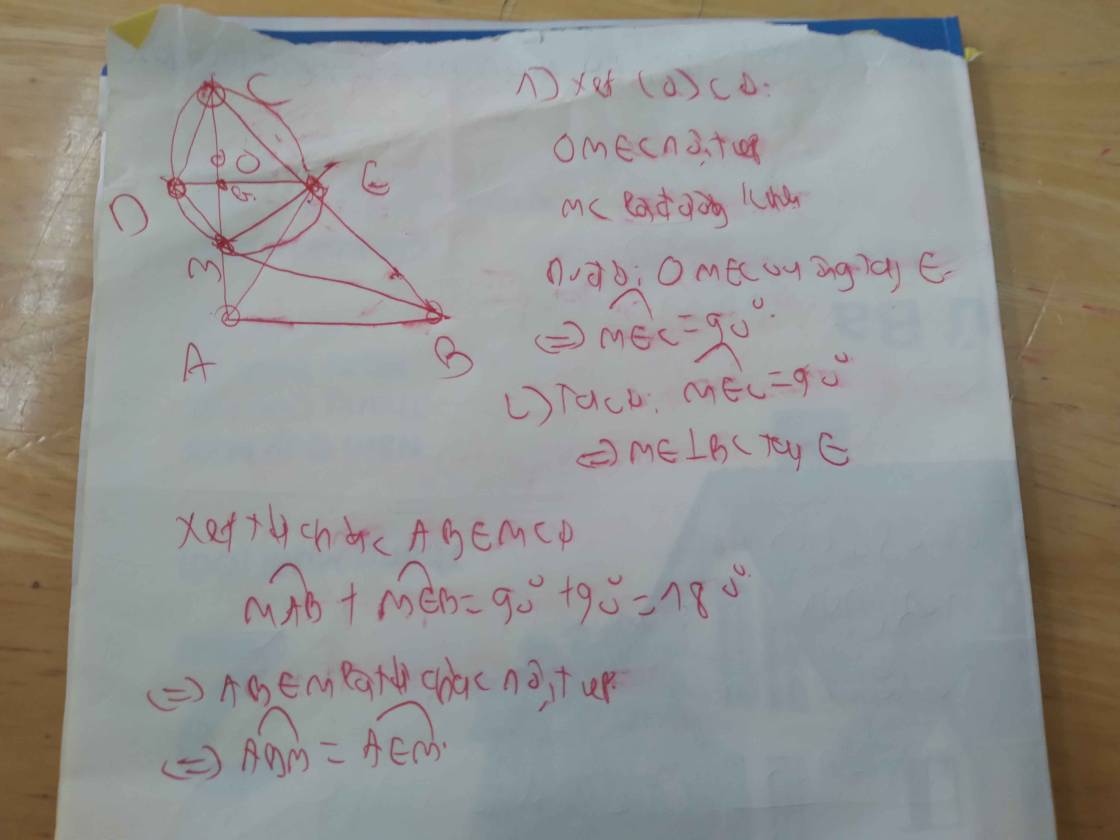
Chứng minh bốn điểm A,B,C,D cùng thuộc một đường tròn. Xác định tâm I của đường tròn này.
Chứng minh rằng: BM.BD=BN.BC.
Gọi J là giao điểm của hai đường thẳng MN và CD. Chứng minh A,B,J thẳng hàng.
Chứng minh rằng: Khi M di động thì tâm của đường tròn ngoại tiếp tam giác AMS thuộc một đường thẳng cố định
Câu 2: Một cái thùng đựng nước được tạo thành từ việc cắt mặt xung quanh của một hình nón bằng một mặt phẳng vuông góc với trục của hình nón. Miệng thùng là đường tròn có bán kính bằng hai lần bán kính mặt đáy của thùng. Bên trong thùng có một cái phễu dạng hình nón có đáy là đáy của thùng có đỉnh là tâm của miệng thùng và có chiều cao bằng 20cm. Biết rằng đổ 5.000 cm3 nước vào thùng thì đầy thùng (nước không chảy được vào bên trong phễu). Tính bán kính đáy r của phễu (giá trị gần đúng của r làm tròn đến hàng phần trăm)
Câu 3: 5x3+6x2+12x+8=0
Câu 4: Một máy kéo nông nghiệp có hai bánh sau to hơn hai bánh trước.Khi bơm căng, bánh xe sau có bán kính hơn bánh xe trước 25cm. Khi đi trên đoạn đường dài 314m thì bánh xe trước quay nhiều hơn bánh xe sau 40 vòng. Tính bán kính theo (cm) của mỗi bánh xe trước và sau, kết quả làm tròn 2 chữ số thập phân. Biết \(\pi\)= 3,14
Câu 5: x2-6x+2m-3=0 (1)
Tìm m để pt (1) có hai nghiệm x1,x2 thỏa mãn : (x12-5x1+2m-4)(x22-5x2+2m-4)=2

Câu 3
5x3+6x2+12x+8=0
<=> x3+6x2+12x+8= -4x3
<=> (x+2)3 = -4x3
<=> (x+2)= \(\sqrt[3]{-4x}\)
<=> x ( 1-\(\sqrt[3]{-4}\))=-2
<=> x= \(\frac{2}{\sqrt[3]{-4}-1}\)