Dùng đồ thị để chứng minh bất đẳng thức giá trị tuyệt đối của x -2>x-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
1
PP
1
1 tháng 7 2018
VP=√(x^2-4x+4)=|x-2|
dt hai nua dt (d1): y=2-x; (x<2);
(d2): y=x-2 (x≥2)
VT: (d3): y=x-3
(d3) nam phia duoi (d1) &(d2) =>VT>VP=>dpcm
NT
1
CH
Cô Hoàng Huyền
Admin
VIP
5 tháng 5 2017
Ta có: \(3mx>x+2\Rightarrow\left(3m-1\right)x>2\left(1\right)\)
Với \(3m-1=0\Rightarrow0>2\): Vô lý nên \(3m-1\ne0.\)
Với \(3m-1>0\Leftrightarrow\Rightarrow m>\frac{1}{3}\Rightarrow x>\frac{2}{3m-1}.\)
Để (1) đúng với mọi x > 1 suy ra\(1\ge\frac{2}{3m-1}\Rightarrow\frac{2}{3m-1}-1\le0\Rightarrow\frac{3-3m}{3m-1}\le0\)
Do 3m - 1 > 0 nên \(3-3m\le0\Rightarrow m\ge1.\)
Kết hợp điều kiện suy ra \(m\ge1.\)
Với \(3m-1< 0\Leftrightarrow\Rightarrow m< \frac{1}{3}\Rightarrow x< \frac{2}{3m-1}.\)
Khi đó không xảy ra trường hợp \(\forall x>1\) thì \(x< \frac{2}{3m-1}.\)
Vậy trường hợp này loại.
Kết luận \(m\ge1.\)
VD
1
CH
Cô Hoàng Huyền
Admin
VIP
3 tháng 4 2018
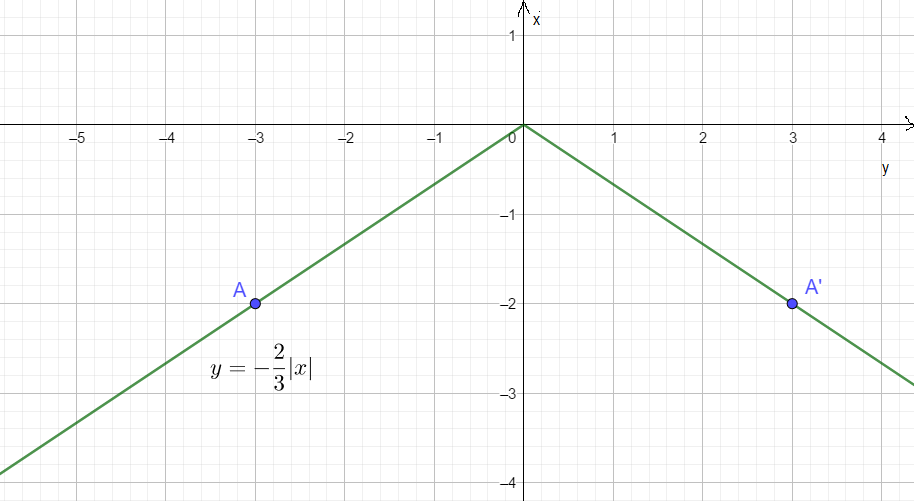
Ta có hàm số: \(y=f\left(x\right)=-\frac{2}{3}\left|x\right|\)
Với \(x\ge0\), ta có hàm số \(y=f\left(x\right)=-\frac{2}{3}x\). Đồ thị hàm số này là một đường thẳng qua gốc tọa độ.
Với \(x< 0\), ta có hàm số \(y=f\left(x\right)=\frac{2}{3}x\). Đồ thị hàm số này là một đường thẳng qua gốc tọa độ.
Ta có bảng giá trị:
| x | -3 | 0 | 3 |
| y = f(x) | -2 | 0 | -2 |
Ta có đồ thị hàm số:
NK
10 tháng 11 2019
a) \(A=\left(x^2-\frac{1}{2}x\right)^2+\frac{3}{4}\left(x+\frac{2}{3}\right)^2+\frac{2}{3}>0\)
Ko biết xét khoảng:v