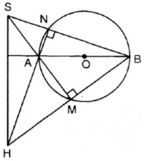
cho đường tròn (O) đường kình AB, lấy điểm S bên ngoài đường tròn sao cho đoạn thẳng SA cắt đường tròn tại M và đoạn thẳng SB cắt đường tròn tại N. gọi H là giao điểm của BM và AN
a. chứng minh tứ giác SMHN nội tiếp
b. chứng minh SM.SA=SN.SB
c. giả sử góc MON=70 độ. tính số đo góc ASB

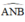 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 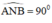 ⇒ AN ⊥ NB
⇒ AN ⊥ NB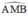 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 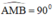 ⇒ AM ⊥ MB
⇒ AM ⊥ MB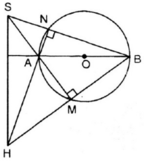
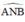 là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 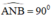 ⇒ AN ⊥ NB
⇒ AN ⊥ NB là góc nội tiếp chắn nửa đường tròn ⇒
là góc nội tiếp chắn nửa đường tròn ⇒ 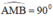 ⇒ AM ⊥ MB
⇒ AM ⊥ MB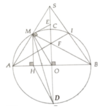
a, Ta có góc SMH=90°; góc SNH=90°( góc nội tiếp chắn 1/2 đường tròn)
xét tứ giác SMHN có
góc SMH+ SNH=90°+90°=180°
suy ra SMHN nội tiếp
b, ta có góc SMN+NMB=90°
góc NBA+NAB=90°
mà góc NMB=NAB (góc nội tiếp chắn cung NB)
suy ra góc SMN = NBA
xét hai tam giác SMN và SBA có
góc S Chung
góc SMN=SBA (cmt)
suy ra hai tam giác đó đồng dạng
suy ra SM/SN=SB/SA
suy ra SM.SA=SN.SB(đpcm)
c,vì góc MON=70° suy ra cung MN=70°(góc ở tâm)
ta có cung AB=180°
mà góc ASB là góc ngoài chắn cung nhỏ MN và cung AB
suy ra góc ASB=(180-70)/2=55°