Mọi người ơi giúp mình với ạ, mình cảm ơn rất nhiều
Trong mặt phẳng tọa độ Oxy có cho đường tròn (C): x2+y2+4x-6y-12=0 và điểm A (2;0) (Aϵ(C)). Viết phương trình đường thẳng đi qua A cắt đường tròn (C) tại điểm thứ hai B sao cho AB = 5\(\sqrt{2}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(C) ⇒ x + 2 2 + y + 3 2 = 25 . Phép vị tự tâm O(0; 0) tỉ số k = 2 biến tâm I(-2; -3) của (C) thành I’(-4; -6), biến bán kính R = 5 thành R’ = 10 ⇒ phương trình (C’) là: x + 4 2 + y + 6 2 = 100
Đáp án C

(C) ⇒ x + 2 2 + y + 3 2 = 25 . Phép vị tự tâm H(1; 0) tỉ số k = 2, biến tâm I(-2; -3) của (C) thành I’(x;y)
⇒ H I ' → = 2 H I →
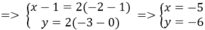
biến bán kính R = 5 thành R’ = 10 ⇒ Phương trình (C’) là: x + 5 2 + y + 6 2 = 100
Đáp án B

( C ) ⇒ ( x − 2 ) 2 + ( y + 3 ) 2 = 16 tâm I(2;-3); bán kính R=4
V H ; − 2 I = I ' x ; y ⇔ H I ' → = − 2 H I →
I’(-1; 15)
R’= |k|R = |-2| . 4 = 8
Vậy phương trình đường tròn (C) là: x + 1 2 + y − 15 2 = 64
Hay x 2 + y 2 + 2 x − 30 y + 162 = 0
Đáp án C
\(\left(C\right):x^2+y^2+4x-6y-12=0\)
\(\Leftrightarrow\left(C\right):\left(x+2\right)^2+\left(y-3\right)^2=25\)
\(\Rightarrow I=\left(-2;3\right)\) là tâm đường tròn, bán kính \(R=5\)
Kẻ IH vuông góc với AB.
\(\Rightarrow IH=\sqrt{R^2-AH^2}=\sqrt{5^2-\dfrac{1}{4}.50}=\dfrac{5\sqrt{2}}{2}\)
Đường thẳng AB có dạng: \(ax+by-2a=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;AB\right)=\dfrac{\left|-2a+3b-2a\right|}{\sqrt{a^2+b^2}}=\dfrac{5\sqrt{2}}{2}\)
\(\Leftrightarrow7a^2-48ab-7b^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=7b\\b=-7a\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}AB:7x+y-14=0\\AB:x-7y-2=0\end{matrix}\right.\)