tìm giá trị lớn nhất của F= -29-4 l3x+8l
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VN
2
MT
22 tháng 6 2015
A=l3x+7l+12( baj này tìm GTNN nha bạn)
vì l3x+7l\(\ge\)0
=>A=l3x+7l+12\(\ge\)12
vậy GTNN của A là 12 tại 3x+7=0
3x=-7
x=-7/3
22 tháng 6 2015
Vì \(!3x+7!\ge0\) với mọi x => \(!3x+7!+12\ge0+12=12\)
Vậy GTNN là 12 khi 3x + 7 = 0 => x = -7/3
Nếu mà GTLN thì x càng lớn thì bt cằng l;ớn Sai đề ròi phải là GTNN cơ
NT
0
NT
0
7 tháng 3 2016
Áp dụng BĐT : \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\) ta được:
P=-|3x-18|-|3x+7|=-|18-3x|-|3x+7|=-(|18-3x|+|3x+7|)\(\le\)-25
Dấu "=" xảy ra khi: (18-3x)(3x+7)\(\ge\)0
Giải cái đó ra bạn sẽ được: -7/3 \(\le x\le\)6
Mà x nguyên nên: x={-2;-1;0;1;2;3;4;5;6} có 9 phần tử
Vậy chọn C
6 tháng 3 2016
Áp dụng \(\left|a\right|-\left|b\right|\le\left|a-b\right|\) (dấu = xảy ra khi a,b > 0), ta có :
\(P=-\left|3x-18\right|-\left|3x+7\right|=-\left|3x-18\right|-\left|7+3x\right|\le-\left|\left(3x-18\right)-\left(7+3x\right)\right|\)
\(=-\left|3x-18-7-3x\right|=-\left|-18-7\right|=-25\)
GTLN của P là -25 <=> 3x - 18 > 0 và 3x + 7 > 0
<=> 3x > 18 và 3x > -7 => x > 6
Vậy có vô số giá trị của x thỏa mãn P có GTLN với điều kiện x > 6 và x là số nguyên
NN
1
CM
17 tháng 10 2017
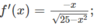
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f CĐ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy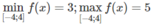 
16 tháng 4 2016
: B=12- l3x+2015l - l-3l = 12- l3x+2015l - 3 = 9 - l3x+2015l
.Có l3x+2015l >= 0 Vx => - l3x+2015l <= 0 Vx
=> 9 - l3x+2015l >= 9
Dấu = xảy ra <=> 3x + 2015 = 0
<=> 3x = -2015
<=> x = -2015 / 3
Vậy Bmax <=> x = -2015 / 3
ND
0
GS
1