Cho điểm M nằm trên tia phân giác At của góc xAy nhọn.Kẻ MH vuông góc với Ax ở H và MK vuông góc với Ay ở K
1.So sánh MH và MK
2.Chứng minh tam giác AMH=tam giác AKM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 1 2017
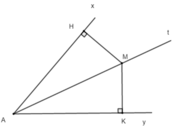
M H ⊥ A x ở H nên MH là khoảng cách từ M đến Ax
M K ⊥ A y ở K nên MK là khoảng cách từ M đến Ay
Mà M thuộc tia phân giác At của góc xAy nên M cách đều hai tia Ax và Ay
Vậy MH = MK.
Chọn đáp án A
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
27 tháng 4 2022
a/
Xét tg MAH và tg BAN có
AM=AB (gt); AN=AH (gt)
\(\widehat{MAH}=\widehat{BAN}\) (góc đối đỉnh)
=> tg MAH = tg BAN (c.g.c)
b/
Ta có tg MAH = tg BAN (cmt) mà \(\Rightarrow\widehat{BNA=}\widehat{MHA}=90^o\)
Xét tg vuông BAN có AB>BN (trong tg vuông cạnh huyền là cạnh có số đo lớn nhất)
Mà AB=AM
=> AM>BN (1)
Xét tg vuông MAH có \(\widehat{MAH}\) là góc nhọn => \(\widehat{MAN}\) là góc tù
Xét tg MAN có MN>AM (trong tg cạnh đối diện với góc tù là cạnh có số đo lớn nhất) (2)
Từ (1) và (2) => MN>BN
Ta có tg MAH = tg BAN (cmt) => \(\widehat{NBM}=\widehat{AMH}\) (3)
Xét tg BMN có
MN>BN (cmt) => \(\widehat{NBM}>\widehat{NMA}\) (trong tg góc đối diện với cạnh có số đo lớn hơn thì lớn hơn góc đối diện với cạnh có số đo nhỏ hơn) (4)
Từ (3) và (4) => \(\widehat{AMH}>\widehat{NMA}\)
c/
Ta có \(\widehat{BNA}=90^o\left(cmt\right)\Rightarrow BN\perp NP\) (1)
Xét tg MNP có \(MH\perp NP\left(gt\right)\) => MH là đường cao
=> MH là đường trung tuyến của tg MNP (trong tg cân đường cao hạ từ đỉnh đồng thời là đường trung tuyến) => HN=HP
Mà IB=IP (gt)
=> IH là đường trung bình của tg BNP => IH//BN (2)
Từ (1) và (2) => \(IH\perp NP\) mà \(MH\perp NP\)
=> M; H; I thảng hàng (từ 1 điểm trên đường thẳng chỉ dựng được duy nhất 1 đường thẳng vuông góc với đường thẳng đã cho)
Xét tg INP có
\(IH\perp NP\) => IH là đường cao của tg INP
HN=HP (cmt) => IH là đường trung tuyến của tg INP
=> tg INP là tg cân tại I (trong tg đường cao đồng thời là đường trung tuyến thì tg đó là tg cân) => IN=IP (cạn bên tg cân)
Mà IP=IB (gt) và IP+IB=BP
=> IN=1/2BP
DT
20 tháng 3 2019
a, xét tam giác AMB và tam giác AMC có:
AB=AC(gt)
\(\widehat{BAM}\) =\(\widehat{CAM}\)(gt)
AM chung
suy ra tam giác AMB= tam giác AMC(c.g.c)
b,xét tam giác AHM và tam giác AKM có:
AM cạnh chung
\(\widehat{HAM}\)=\(\widehat{KAM}\)(gt)
suy ra tam giác AHM=tam giác AKM(CH-GN)
Suy ra AH=AK
c,gọi I là giao điểm của AM và HK
xét tam giác AIH và tam giác AIK có:
AH=AK(theo câu b)
\(\widehat{IAH}\)=\(\widehat{IAK}\)(gt)
AI chung
suy ra tam giác AIH=tam giác AIK (c.g.c)
Suy ra \(\widehat{AIH}\)=\(\widehat{AIK}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{AIH}\)=\(\widehat{AIK}\)= 90 độ
\(\Rightarrow\)HK vuông góc vs AM