Giải phương trình sau bằng mọi cách (ko sử dụng máy tính nhé)
\(x^3-3x+1=0\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có đồ thị:
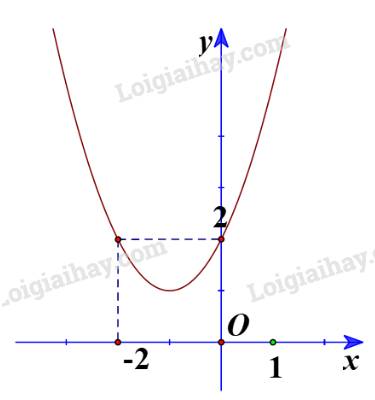
Từ đồ thị ta thấy \({x^2} + 2x + 2 > 0\) biểu diễn phần parabol \(y = {x^2} + 2x + 2\) nằm phía trên trục hoành, tương ứng với mọi \(x \in \mathbb{R}\).
Vậy tập nghiệm của bất phương trình \({x^2} + 2x + 2 > 0\) là \(\mathbb{R}\).
b) Ta có đồ thị:
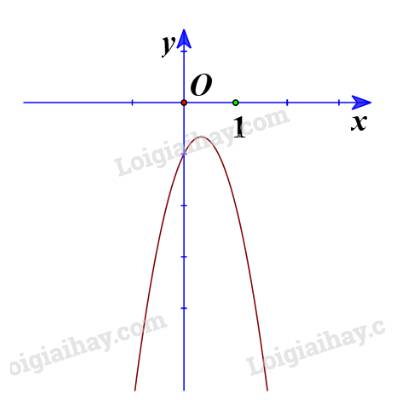
Từ đồ thị ta thấy \( - 3{x^2} + 2x - 1 > 0\) biểu diễn phần parabol \(y = - 3{x^2} + 2x - 1\) nằm phía trên trục hoành, tương ứng với \(x \in \emptyset \)
Vậy tập nghiệm của bất phương trình \( - 3{x^2} + 2x - 1 > 0\) là \(\emptyset \).

a, (3x+1)(7x+3)=(5x-7)(3x+1)
<=> (3x+1)(7x+3)-(5x-7)(3x+1)=0
<=> (3x+1)(7x+3-5x+7)=0
<=> (3x+1)(2x+10)=0
<=> 2(3x+1)(x+5)=0
=> 3x+1=0 hoặc x+5=0
=> x= -1/3 hoặc x=-5
Vậy...
a) (3x - 2)(4x + 5) = 0
⇔ 3x - 2 = 0 hoặc 4x + 5 = 0
1) 3x - 2 = 0 ⇔ 3x = 2 ⇔ x = 2/3
2) 4x + 5 = 0 ⇔ 4x = -5 ⇔ x = -5/4
Vậy phương trình có tập nghiệm S = {2/3;−5/4}
b) (2,3x - 6,9)(0,1x + 2) = 0
⇔ 2,3x - 6,9 = 0 hoặc 0,1x + 2 = 0
1) 2,3x - 6,9 = 0 ⇔ 2,3x = 6,9 ⇔ x = 3
2) 0,1x + 2 = 0 ⇔ 0,1x = -2 ⇔ x = -20.
Vậy phương trình có tập hợp nghiệm S = {3;-20}
c) (4x + 2)(x2 + 1) = 0 ⇔ 4x + 2 = 0 hoặc x2 + 1 = 0
1) 4x + 2 = 0 ⇔ 4x = -2 ⇔ x = −1/2
2) x2 + 1 = 0 ⇔ x2 = -1 (vô lí vì x2 ≥ 0)
Vậy phương trình có tập hợp nghiệm S = {−1/2}
d) (2x + 7)(x - 5)(5x + 1) = 0
⇔ 2x + 7 = 0 hoặc x - 5 = 0 hoặc 5x + 1 = 0
1) 2x + 7 = 0 ⇔ 2x = -7 ⇔ x = −7/2
2) x - 5 = 0 ⇔ x = 5
3) 5x + 1 = 0 ⇔ 5x = -1 ⇔ x = −1/5
Vậy phương trình có tập nghiệm là S = {−7/2;5;−1/5}

5x2 – 3x – 7 = 0
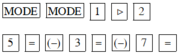
Màn hình hiện x1 = 1,520655562
Ấn tiếp  , màn hình hiện x2 = –0,9206555616
, màn hình hiện x2 = –0,9206555616
Vậy nghiệm gần đúng của phương trình là: x1 = 1,52; x2 = –0,92

3 x − 2 y = 5 2 x + y = 8 ⇔ 3 x − 2 y = 5 4 x + 2 y = 16 ⇔ 7 x = 21 2 x + y = 8 ⇔ x = 3 2 x + y = 8 ⇔ x = 3 y = 2

3x3 - 3x2- 6x = 0
x ( 3x2 - 3x - 6 ) = 0
x [ 3x2 + 3x - 6x - 6 ] = 0
x [ 3x ( x + 1 ) - 6 ( x + 1 ) ] = 0
x ( 3x - 6 ) ( x + 1 ) = 0
<=> x = 0 hoặc 3x - 6 = 0 hoặc x + 1 = 0
1) x = 0
2) 3x - 6 = 0 <=> x = 2
3) x + 1 = 0 <=> x = -1
Vậy taaph nghiệm của phương trình đã cho S={0 : -1 : 2 }
\(3x^3-3x^2-6x=0\)
\(3x^3-6x^2+3x^2-6x=0\)
\(3x^2.\left(x-2\right)+3x\left(x-2\right)=0\)
\(\left(3x^2+3x\right)\left(x-2\right)=0\)
\(3x\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow3x=0\) \(\Rightarrow x=0\)hoặc \(\orbr{\begin{cases}x+1=0\\x-2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)
\(lim_{x\rightarrow+\infty}\left(\sqrt{ax^2+bx}-cx\right)=-2\)
\(\Leftrightarrow\sqrt{ax^2+bx}-cx=-2\left(x\rightarrow+\infty\right)\)(1)
\(\Leftrightarrow\frac{ax^2+bx-c^2x^2}{\sqrt{ax^2+bx}+cx}=-2\left(x\rightarrow+\infty\right)\)
\(\Leftrightarrow\frac{x\left(ax+b-c^2x\right)}{x\sqrt{a+\frac{b}{x}}+c}=-2\left(x\rightarrow+\infty\right)\)
\(\Leftrightarrow\frac{x\left(a-c^2\right)+b}{\sqrt{a}+c}=-2 \left(x\rightarrow+\infty\right)\)
\(\Rightarrow x\left(a-c^2\right)+b=-2\left(\sqrt{a}+c\right) \left(x\rightarrow+\infty\right)\)
\(\Leftrightarrow a-c^2=\frac{-2\left(\sqrt{a}+c\right)-b}{x}\left(x\rightarrow+\infty\right)\)
\(\Rightarrow a-c^2=0\Leftrightarrow a=c^2\)
Mà \(c^2+a=18\)suy ra \(\hept{\begin{cases}c=\pm3\\a=9\end{cases}}\)
TH1: c=-3;a=9 thì (1) có giới hạn là vô cùng (loại)
TH2: c=3; a=9 thì (1) tương đương
\(\sqrt{9x^2+bx}-3x=-2\left(x\rightarrow+\infty\right)\)
\(\Leftrightarrow\frac{bx}{x\left(\sqrt{9+\frac{b}{x}}+3\right)}=-2\left(x\rightarrow+\infty\right)\)
\(\Leftrightarrow\frac{b}{6}=-2\Rightarrow b=-12\)
\(\Rightarrow a+b+5c=9-12+5.3=12\)
Giả sử cạnh hình vuông là a
\(AM=\frac{a}{2}\)
\(AN=\frac{3a\sqrt{2}}{4}\)
\(MN=\sqrt{\left(2-1\right)^2+\left(-1-2\right)^2}=\sqrt{10}\)
\(Cos\widehat{MAN}=\frac{AM^2+AN^2-MN^2}{2AM.AN}\)
\(\Leftrightarrow\frac{\sqrt{2}}{2}=\frac{\frac{1}{4}a^2+\frac{9}{8}a^2-10}{2.\frac{1}{2}a.\frac{3\sqrt{2}}{4}a}\Rightarrow a=4\)
Giả sử CD: \(\left(d\right):y=ax+b\)
MN cắt CD tại K \(\Rightarrow K\in\left(d\right)\)
Ta có:
\(\Delta MNA\infty\Delta KNC\)
\(\Rightarrow\frac{MN}{NK}=\frac{AN}{NC}=3\)
\(\Leftrightarrow\overrightarrow{MN}=3\overrightarrow{NK}\Rightarrow K\left(\frac{7}{3};-2\right)\)
Do \(K\in\left(d\right)\Rightarrow7a+3b=-6\)(1)
Viết lại \(\left(d\right):ax-y+b=0\)
\(d_{\left(M,\left(d\right)\right)}=4\Rightarrow\frac{\left|a-2+b\right|}{\sqrt{a^2+1}}=4\Leftrightarrow\left(a-2+b\right)^2=16\left(a^2+1\right)\)(2)
Từ (1) và (2) \(\hept{\begin{cases}a=0\\b=-2\end{cases}}\)hoặc \(\hept{\begin{cases}a=\frac{3}{4}\\b=-\frac{15}{4}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\left(d\right):y+2=0\\\left(d\right):3x-4y-15=0\end{cases}}\)