Tính:
a) (2+3i)2
b) (2+3i)3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với ![]()
![]() Khi đó
Khi đó
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dấu bằng đạt tại
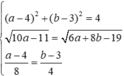
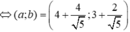
⇒ a - 2 b = - 2
Chọn đáp án B.
Mẹo trắc nghiệm: Có
![]()
![]()
![]()
Khi đó
![]()
![]()
![]()
![]()
![]()
Khi đó a-2b![]()
Chọn đáp án B.

Đáp án A.
Phương pháp:
Từ z = z ¯ + 4 - 3 i tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z = x + yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất ó MA = MB
Cách giải: Gọi z = x + ui ta có:
![]()
![]()
![]()
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(–1;1); B(2; –3) ta có:
|z+1–i|+|z–2+3i| = MA + MB nhỏ nhất.
Ta có: ![]() dấu bằng xảy ra ó MA = MB => M thuộc trung trực của AB.
dấu bằng xảy ra ó MA = MB => M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có 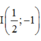 và
A
B
→
=
3
;
-
4
và
A
B
→
=
3
;
-
4
Phương trình đường trung trực của AB là 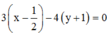
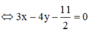
Để (MA + MB)min ó Tọa độ điểm M là nghiệm của hệ phương trình
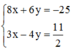
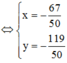
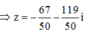


Đáp án A.
Phương pháp:
Từ ![]() tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất
nhỏ nhất
![]()
Cách giải: Gọi z=x+ui ta có:
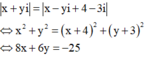
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất.
nhỏ nhất.
Ta có: ![]()
Dấu bằng xảy ra ![]()
![]() M thuộc trung trực của AB.
M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có ![]()
Phương trình đường trung trực của AB là
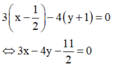
Để ![]()
![]() Tọa độ điểm M là nghiệm của hệ phương trình
Tọa độ điểm M là nghiệm của hệ phương trình


a ) 2|x - 3| - 5 = 3 <=> 2|x - 3| = 8 <=> |x - 3| = 4 => x - 3 = ± 4
TH1 : x - 3 = 4 => x = 7
TH2 : x - 3 = - 4 => x = - 1
Vậy x = { - 1; 7 }
b ) 2|2x + 3| + |2x + 3| = 6 <=> 3|2x + 3| = 6 => |2x + 3| = 2 => 2x + 3 = ± 2
=> x = { - 5/2 ; - 1/2 }
c ) 3|x + 1|2 + |x + 1|2 = 16
4|x + 1|2 = 16
=> |x + 1|2 = 4 = 22 ( ko xét TH |x + 1| = - 2 vì |x + 1| ≥ 0 )
=> |x + 1| = 2 => x + 1 = ± 2 => x = { - 3; 1 }

a/ \(\left(2-3i\right)\left(2+3i\right)=4-9i^2=4+9=13\)
b/ \(\left(2+3i\right)\left(4-i\right)=8-2i+12i-3i^2=11+10i\)
c/ \(=\dfrac{\left(1+i\right)\left(2+3i\right)}{4-9i^2}=\dfrac{2+5i-3}{4+9}=\dfrac{5i-1}{13}\)

a) ( 3 - 4 i ) 2 = 3 2 − 2.3.4i + ( 4 i ) 2 = −7 − 24i
b) ( 2 + 3 i ) 3 = 2 3 + 3. 2 2 .3i + 3.2. ( 3 i ) 2 + ( 3 i ) 3 = −46 + 9i
c) [ ( 4 + 5 i ) – ( 4 + 3 i ) ] 5 = ( 2 i ) 5 = 32i
d) ( 2 - i 3 ) 2 = −1 − 2i 6
Ta có: (2+3i)2=(2+3i)(2+3i)=(22-33 )+(2.2.3)i=-5+12i
Tổng quát (a+bi)2=a2-b2+2abi
Ta có: (2+3i)3 =(2+3i)
(2+3i)2=(-5+12i)(2+3i)
=(-5.2-12.3)+(-5.3+12.2)i=-49+9i
Có thể tính ((2+3i)3 bằng cách áp dụng hẳng đẳng thức
(2+3i)3=23+3.22.3i+3.2.(3i)2+(3i)3
=(8-54)+(36-27)i=-46+9i