Cho góc bẹt xOy . Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om , On . Sao cho xOm = a độ và yOn = 70 độ . Tìm giá trị của a để tia on là tia phân giác của yOn Help me , please . Tick nhah
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 6 2022
Để On là phân giác của góc yOm thì \(\widehat{yOn}=\dfrac{1}{2}\widehat{yOm}\)
=>\(\widehat{yOm}=140^0\)
=>\(a=180^0-140^0=40^0\)
CM
30 tháng 10 2018
Đáp án là D
Vì tia On là tia phân giác của ∠yOm nên ∠yOm = 2.∠yOn = 2. 70 0 = 140 0
Lại có xOy là góc bẹt nên ∠xOm và ∠yOm là hai góc kề bù
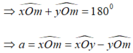
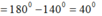
Vậy a = 40 0
MN
9 tháng 7 2021
a) Vì ˆxOyxOy^ là góc bẹt
⇒ Ox và Oy là 2 tia đối nhau
⇒ Tia On nằm giữa 2 tia Ox và Oy
⇒ˆxOn+ˆyOn=ˆxOy
⇒ˆxOn+150o=180o
⇒ˆxOn=30o
Trên cùng 1 nửa mặt phẳng bờ xy, ta có:
ˆxOn<ˆxOm(30o<60o)
⇒ Tia On nằm giữa 2 tia Ox và Om
⇒ˆxOn+ˆmOn=ˆxOm
⇒30o+ˆmOn=60o
⇒ˆmOn=30o
b) Ta có: ˆxOn=ˆmOn(=30o)
Lại có: Tia On nằm giữa 2 tia Ox và Om
⇒ Tia On là tia phân giác của ˆxOm
10 tháng 8 2019
Bài làm
Ta có: \(\widehat{xOy}=\widehat{xOm}+\widehat{yOn}+\widehat{mOz}+\widehat{zOn}\)
Mà \(\widehat{xOm}=\widehat{yOn}=2\widehat{xOm}\)
Oz là tia phân giác của \(\widehat{mOn}\)
=> \(\widehat{mOz}=\widehat{zOn}=2\widehat{mOz}\)
=> \(\widehat{xOy}=2\widehat{xOm}+2\widehat{mOz}\)
Hay \(180^0=2\widehat{xOm}+2\widehat{mOz}\)
=> \(180^0=2(\widehat{xOm}+\widehat{mOz})\)
=> \(\widehat{xOm}+\widehat{mOz}=180^0:2\)
=> \(\widehat{xOm}+\widehat{mOz}=90^0\)
Hay \(\widehat{xOz}=90^0\)
=> \(Oz\perp xy\)
Vậy \(Oz\perp xy\)( đpcm )
# Học tốt #
YN
20 tháng 5 2021
\(A)\)
\(B)\)
Theo đề ra: Góc xOy là góc bẹt => Góc xOy = 180 độ
Góc xOm = 60 độ
=> Góc xOy > góc xOm => Tia Om nằm giữa hai tia Ox và Oy
Ta có: mOy = xOy - xOm
mOy = 180 độ - 60 độ
mOy = 120 độ
Ta có: mOn = yOn - mOy
mOn = 150 độ - 120 độ
mOn = 30 độ
\(C)\)
Ta có: xOn = xOm - mOn
xOn = 60 độ - 30 độ
xOn = 30 độ
=> Góc xOn = góc mOn
=> Tia On là tia phân giác của góc xOm