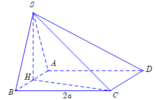
cho hình chóp SABCD đáy là hình vuông cạnh 2a. (SAB) vuông góc (ABCD). Tam giác SAB là tam giác cân tại S. Tính thể tích SABCD biết a)Góc giữa SA và đáy là alpha biết tan alpha=2 b)Góc giữa SC và đáy là alpha biết tan alpha= căn 5 c)Góc giữa (SCD) và (ABCD) là alpha biết tan alpha=3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HP
17 tháng 6 2021
Kẻ SH vuông góc AB tại H.
a, Ta có: \(h=SH=AH.tan\alpha=2a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.2a=\dfrac{8a^3}{3}\)
b, \(SB=BC.tan\alpha=2\sqrt{5}a\Rightarrow SH=\sqrt{SB^2-BH^2}=\sqrt{19}a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.\sqrt{19}a=\dfrac{4\sqrt{19}a^3}{3}\)
c, Kẻ HI vuông góc với CD.
Ta có: \(SH=HI.tan\alpha=6a\)
\(\Rightarrow V=\dfrac{1}{3}.B.h=\dfrac{1}{3}.\left(2a\right)^2.6a=8a^3\)
AH
Akai Haruma
Giáo viên
22 tháng 6 2021
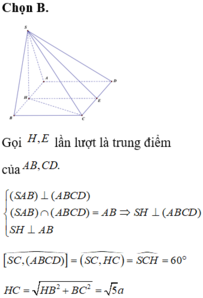
Lời giải:
Lấy $H$ là trung điểm $AB$ thì do $SAB$ cân tại $S$ nên $SH\perp BH$
$BH$ là giao tuyến của $(SAB), (ABCD)$; (SAB)\perp (ABCD)$ nên $SH\perp (ABCD)$
$\Rightarrow (SC, (ABCD))=(SC, CH)=\widehat{SCH}=45^0$
$\Rightarrow SH=CH=\sqrt{BC^2+BH^2}=\sqrt{(2a)^2+(\frac{a}{2})^2}=\frac{\sqrt{17}}{2}a$
\(V_{S.ABCD}=\frac{1}{3}.SH.S_{ABCD}=\frac{1}{3}.\frac{\sqrt{17}}{2}a.a.2a=\frac{\sqrt{17}}{3}a^3\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 4 2021
\(\left\{{}\begin{matrix}\left(SAB\right)\perp\left(ABCD\right)\\\left(SAB\right)\cap\left(ABCD\right)=AB\\SA\perp AB\end{matrix}\right.\) \(\Rightarrow SA\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(\widehat{SBA}=45^0\) (do SAB vuông cân tại A)
b.
\(\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=AB\sqrt{2}=2a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{SC}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SCA}\approx35^015'\)
CM
18 tháng 10 2018
Đáp án là A.
V S . A B C D = 4 a 3 3 = 1 3 .4 a 2 . S H
S C = S H 2 + H C 2 = S H 2 + B H 2 + B C 2 = a 6 .
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 5 2021
Kẻ \(SH\perp AB\Rightarrow SH\perp\left(ABCD\right)\)
Trong mp (ABCD), qua H kẻ đường thẳng song song AD cắt CD tại K
\(\Rightarrow\left\{{}\begin{matrix}AB\perp\left(SHK\right)\\CD\perp\left(SHK\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(SHK\right)\perp\left(SAB\right)\\\left(SHK\right)\perp\left(SCD\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{HSK}\) là góc giữa (SAB) và (SCD)
Ta có:
\(SB=\sqrt{AB^2-SA^2}=a\sqrt{3}\Rightarrow SH=\dfrac{SA.SB}{AB}=\dfrac{a\sqrt{3}}{2}\); \(HK=AD=2a\)
\(tan\widehat{HSK}=\dfrac{HK}{SH}=\dfrac{4\sqrt{3}}{3}\Rightarrow\widehat{HSK}\approx66^035'\)
