cho tam giác ABC cân có AB=AC=12cm , đường cao AH,I là hình chiếu của H trên AC
Tính độ dài CI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 8 2016
a) Dễ dàng c/m được tam giác HIC đồng dạng với tam giác AHC (g.g)
=> \(\frac{HC}{AC}=\frac{IC}{HC}\Rightarrow IC=\frac{HC^2}{AC}=\frac{\left(\frac{BC}{2}\right)^2}{AC}\) . Bạn thay số vào tính.
b) Dễ dàng c/m được HI là đường trung bình tam giác BKC => I nằm giữa K và C
Lại có I nằm giữa AC => K nằm giữa A và C
16 tháng 8 2016
a) \(IC=\frac{HC^2}{AC}=\frac{6^2}{9}=4\) (cm)
b) \(\Delta ABC\) cân tại điểm A.
\(\Rightarrow\widehat{B}=\widehat{C}\) là góc nhọn
=> A nằm trên mặt phẳng chứa A bờ BC.
\(\Rightarrow\Delta AHC\approx\Delta BKC\)
\(\Rightarrow\frac{AC}{BC}=\frac{HC}{KC}\)
\(\Rightarrow KC=\frac{12.6}{9}=8< 9\)
Vậy K nằm giữa A và C
9 tháng 9 2019
Áp dụng định lí Py-ta-go cho hai tam giác vuông AKH và AIH, ta có:
\(AK^2+HK^2=AH^2\)
\(AI^2+HI^2=AH^2\)
\(\Rightarrow AK^2+HK^2=AI^2+HI^2\) \(\left(\cdot\right)\)
Giả sử \(AB\ne AC\)ta xét 2 trường hợp:
T/hợp 1: \(AB>AC\)
\(\Rightarrow AB-BK>AC-CI\)( vì \(BK=CI\)) hay \(AK>AI\) \(\left(1\right)\)
Mặt khác, vì \(AB>AC\)nên \(HB>HC\)( quan hệ đường xiên - hình chiếu )
\(\Rightarrow HB^2>HC^2\)hay \(HK^2+BK^2>HI^2+CI^2\Rightarrow HK>HI\) \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)suy ra: \(AK^2+HK^2>AI^2+HI^2\): trái với \(\left(\cdot\right)\)
T/hợp 2: \(AB< AC\): Chứng minh tương tự ta có: \(AK^2+HK^2< AI^2+HI^2\): trái với \(\left(\cdot\right)\)
Vậy điều giả sử \(AB\ne AC\)là sai, hay \(AB=AC\)
H9
HT.Phong (9A5)
CTVHS
8 tháng 8 2023
a) Ta có: \(BC=13cm\Rightarrow BC^2=13^2cm=169cm\)
Xét: \(AB^2+AC^2=5^2+12^2=25+144=169=13^2=BC^2\)
Vậy tam giác ABC vuông tại A có cạnh huyền BC
b) Áp dụng định lý thích hai cạnh góc vuông tà tích giữa cạnh huyền và đường cao ta có:
\(AH\cdot BC=AB\cdot AC\)
\(\Rightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12\cdot5}{13}\approx4,6\left(cm\right)\)
c) Xét ΔAHB vuông tại H có đường cao HE ta có:
\(\Rightarrow AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại H có đường cao HF ta có:
\(\Rightarrow AH^2=AF\cdot AC\) (2)
Từ (1) và (2)
\(\Rightarrow AB\cdot AE=AC\cdot AF\)
\(\Rightarrow\dfrac{AB}{AF}=\dfrac{AC}{AE}\) (3)
Dựa vào (3)
Ta suy ra: \(\Delta AEF\sim\Delta ABC\)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) (đpcm)
8 tháng 8 2023
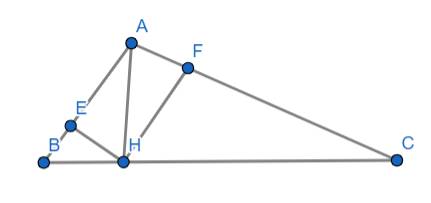
a: Xét ΔÂBC có BC^2=AB^2+AC^2
nên ΔABC vuông tại A
b: AH=AB*AC/BC=60/13(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên AE*AB=AH^2
ΔAHC vuông tại H có HF là đường cao
nên AF*AC=AH^2
=>AE*AB=AF*AC
=>AE/AC=AF/AB
=>ΔAEF đồng dạng với ΔACB
=>góc AFE=góc ABC
