tìm các giá trị của x để :A=5*x+4/x2+1
a)A=0; b)A>0; c)A<0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a)\dfrac{5x+4}{x^2+1}=0\)
\(\Rightarrow5x+4=0\)
\(\Rightarrow x=-\dfrac{4}{5}\)
Vậy \(A=0\Leftrightarrow x=-\dfrac{4}{5}\)
\(b)\dfrac{5x+4}{x^2+1}>0\)
Do \(x^2+1>0\forall x\)
\(\Rightarrow5x+3>0\)
\(\Rightarrow x>-\dfrac{4}{5}\)
Vậy \(A>0\Leftrightarrow x>-\dfrac{4}{5}\)
\(c)\dfrac{5x+4}{x^2+1}< 0\)
Do \(x^2+1>0\forall x\)
\(\Rightarrow5x+4< 0\)
\(\Rightarrow x< -\dfrac{4}{5}\)
Vậy \(A< 0\Leftrightarrow x< -\dfrac{4}{5}\)

\(1,\\ a,\dfrac{x^2}{x+1}+\dfrac{x}{x+1}=\dfrac{x^2+x}{x+1}=\dfrac{x\left(x+1\right)}{x+1}=x\)
\(b,\left(\dfrac{2xy}{x^2-y^2}+\dfrac{x-y}{2x+2y}\right):\dfrac{x+y}{2x}=\left(\dfrac{4xy}{2\left(x-y\right)\left(x+y\right)}+\dfrac{\left(x-y\right)^2}{2\left(x-y\right)\left(x+y\right)}\right).\dfrac{2x}{x+y}=\dfrac{4xy+x^2-2xy+y^2}{2\left(x-y\right)\left(x+y\right)}.\dfrac{2x}{x+y}=\dfrac{2x\left(x^2+2xy+y^2\right)}{2\left(x-y\right)\left(x+y\right)^2}=\dfrac{2x\left(x+y\right)^2}{2\left(x-y\right)\left(x+y\right)^2}=\dfrac{x}{x-y}\)

a) Rút gọn thu được B = 4 x ( 2 + x ) ( 2 − x ) ( 2 + x ) : x − 3 x ( 2 − x ) = 4 x 2 x − 3 với x ≠ ± 2 ; x ≠ 0 ; x ≠ 3
b) 4 x 2 x − 3 < 0 ⇔ x − 3 < 0 ⇔ x < 3 ;
Kết hợp điều kiện được 0 < x < 3; x ≠ ± 2.

a: ĐKXĐ: x+1<>0
=>x<>-1
b: x^2+x=0
=>x=0(nhận) hoặc x=-1(loại)
Khi x=0 thì \(A=\dfrac{2\cdot0-3}{0+1}=-3\)
c: Để A nguyên thì 2x-3 chia hết cho x+1
=>2x+2-5 chia hết cho x+1
=>-5 chia hết cho x+1
=>\(x+1\in\left\{1;-1;5;-5\right\}\)
=>\(x\in\left\{0;-2;4;-6\right\}\)
d: Để A>0 thì (2x-3)/(x+1)>0
=>x>3/2 hoặc x<-1

Điều kiện x ≠ 2 và x ≠ 0
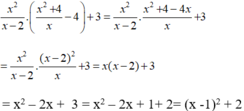
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.

Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)

a: Khi x=9 thì A=(9-2)/(3+2)=7/5
b: \(B=\dfrac{x-\sqrt{x}+2\sqrt{x}+2-4}{x-1}=\dfrac{x+\sqrt{x}-2}{x-1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
c: P=A*B
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{x-2}{\sqrt{x}+2}=\dfrac{x-2}{\sqrt{x}+1}\)
P=7/4
=>(x-2)/(căn x+1)=7/4
=>4x-8=7căn 7+7
=>4x-7căn x-15=0
=>căn x=3(nhận) hoặc căn x=-5/4(loại)
=>x=9

Phân thức 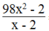 = 0 khi
98
x
2
+
2
=
0
và x – 2
≠
0
= 0 khi
98
x
2
+
2
=
0
và x – 2
≠
0
Ta có: x – 2 ≠ 0 ⇔ x ≠ 2
98 x 2 + 2 = 0 ⇔ 2 49 x 2 - 1 = 0 ⇔ (7x + 1)(7x – 1) = 0
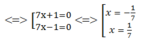
Ta có: 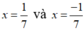 thỏa mãn điều kiện x
≠
2
thỏa mãn điều kiện x
≠
2
Vậy ![]() thì phân thức
thì phân thức ![]() có giá trị bằng 0.
có giá trị bằng 0.
Nhóm thành tích
\(A = (x+1)(5x^2-4x+4)/ x^2\)
A=0 => x= -1 Hoặc
\( 5x^2-4x+4=0\)
Nhưng \( 5x^2-4x+4>0\) Luôn > 0 vì
Nhóm \( 5x^2-4x+4 = 5 (x-2/5)^2 + 16/5\) luôn >0
A>0 => x+1 > 0 => x>-1 Và
\( 5x^2-4x+4>0\) Luôn > 0 Đã chứng minh ở trên
A<0 thì x<-1