Cho hình chóp tứ giác đều SABCD có cạnh đáy bằng 10cm trung đoanh bằng 13cm
a) Tính độ dài cạnh bên
b) Tính diện tích xung quanh hình chóp
c) Tính thể tích hình chóp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chu vi đáy là:
8*4=32(cm)
Diện tích xung quanh là:
\(32\cdot10=320\left(cm^2\right)\)

Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)

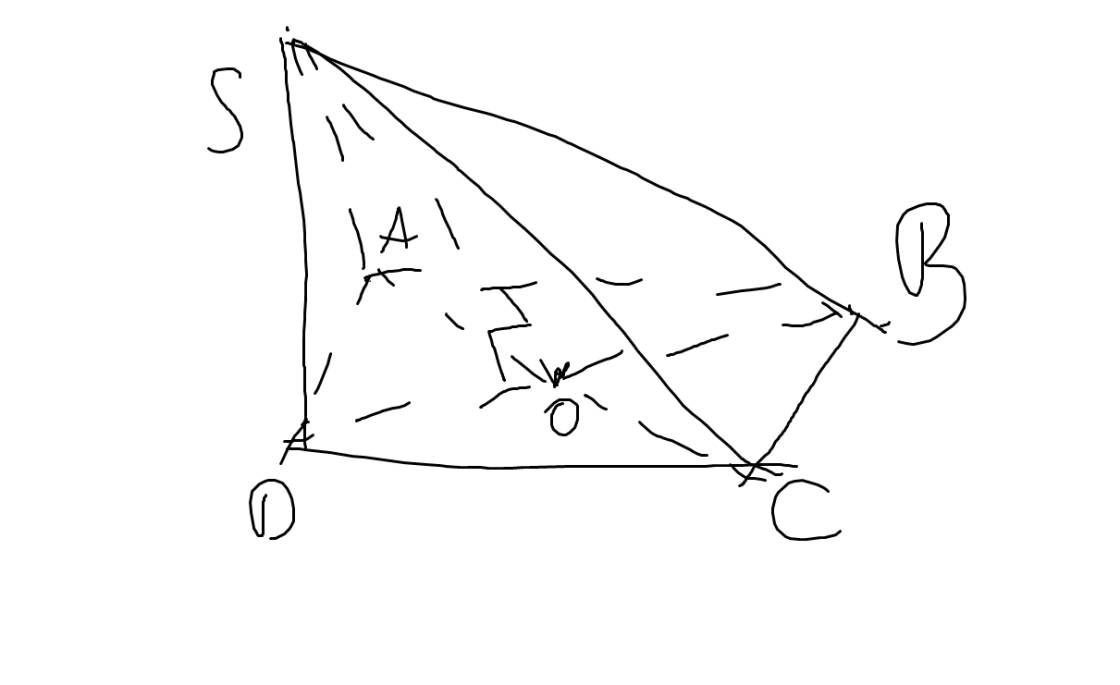
Trong hình chóp tứ giác đều, đường cao kẻ từ đỉnh xuống đáy có chân đường cao là tâm của đáy và đường cao đó chính là trung đoạn của hình chóp
a: Vẽ SO\(\perp\)(ABCD)
=>SO là trung đoạn của hình chóp ABCD và O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
ABCD là hình vuông
=>\(AC=BD=\sqrt{4^2+4^2}=4\sqrt{2}\left(cm\right)\)
=>\(AO=BO=CO=DO=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\left(cm\right)\)
SO vuông góc (ABCD)
=>SO vuông góc OD
=>ΔSOD vuông tại O
=>\(SO^2+OD^2=SD^2\)
=>\(SO^2=6^2-8=28\)
=>\(SO=2\sqrt{7}\left(cm\right)\)
b: \(S_{Xq}=p\cdot d=C_{đáy}\cdot SO=4\cdot4\cdot2\sqrt{7}=32\sqrt{7}\left(cm^2\right)\)
c: \(S_{tp}=S_{xq}+S_{đáy}\)
\(=32\sqrt{7}+4^2=32\sqrt{7}+16\left(cm^2\right)\)
Bạn tự vẽ hình nha
a, Gọi \(O=BD\cap AC\)
K là trung điểm của CD
\(\Rightarrow OK=\dfrac{1}{2}AD=\dfrac{1}{2}CD=5\)
b, \(S_{xq}=\left(AB+BC\right).SK\)
\(=\left(10+10\right).13\)
\(=260\left(cm^2\right)\)
c, \(V_{S_{ABCD}}=\dfrac{1}{3}.SO.SB.SC\)
\(=\dfrac{1}{3}.12.10.10\)
\(=400\left(cm^3\right)\)
-Chúc bạn học tốt-
bạn thiếu r nè, chưa tính SO