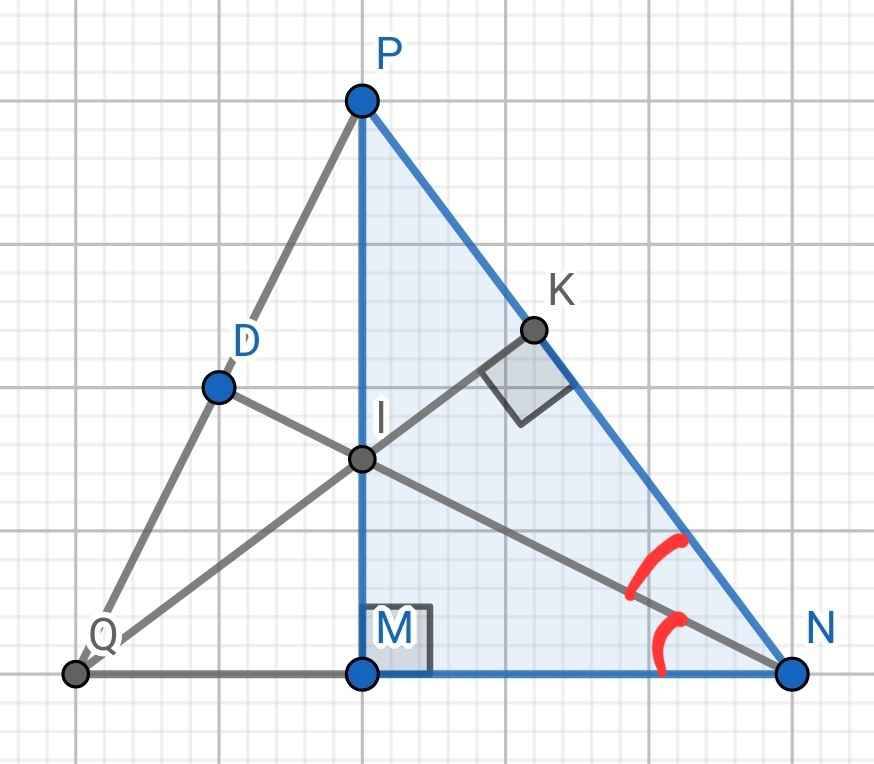
Cho tam giác MNP cân tại M có đường trung tuyến MI.
a) Chứng minh MI ⊥ NP.
b) Kẻ IQ vuông góc MN (Q thuộc MN) IK vuông góc MP (K thuộc MP ) . Chứng minh IQ = IK và IM là đường trung trực của QK.
c) Trên tia đối tia QI lấy điểm E sao cho QE = QI, trên tia đối tia KI lấy điểm F sao cho
KF=KI. Chứng minh tam giác MEF cân.
d) Chứng minh FE // NP
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP

a: Xét tứ giác MKIE có
\(\widehat{MKI}=\widehat{MEI}=\widehat{EMK}=90^0\)
Do đó: MKIE là hình chữ nhật
b: Xét ΔMPN có
I là trung điểm của NP
IK//MP
Do đó: K là trung điểm của MN
Ta có: K là trung điểm của MN
mà IK⊥MN
nên IK là đường trung trực của MN

a: Xét ΔNMI vuông tại M và ΔNKI vuông tại K co
NI chung
góc MNI=góc KNI
=>ΔNMI=ΔNKI
b: Xet ΔIMA vuông tại M và ΔIKP vuông tại K có
IM=IK
góc MIA=góc KIP
=>ΔIMA=ΔIKP
=>KI=IM
=>KI<IA

Tự kẻ hình nha
a) - Vì tam giác MNP cân tại M (gt)
=> MN = MP (định nghĩa)
góc MNP = góc MPN (dấu hiệu)
- Vì NH vuông góc với MP (gt)
=> tam giác NHP vuông tại H
- Vì PK vuông góc với MN (gt)
=> tam giác PKN vuông tại K
- Xét tam giác vuông NHP và tam giác vuông PKN, có:
+ Chung NP
+ góc HPN = góc KNP (cmt)
=> tam giác vuông NHP = tam giác vuông PKN (cạnh huyền - góc nhọn)
b) Vì tam giác vuông NHP = tam giác vuông PKN (cmt)
=> góc HNP = góc KPN (2 góc tương ứng)
=> tam giác ENP cân tại E (dấu hiệu)
c) - Vì tam giác ENP cân tại E (cmt)
=> EN = EP (định nghĩa)
- Xét tam giác MNE và tam giác MPE, có:
+ Chung ME
+ MN = MP (cmt)
+ EN = EP (cmt)
=> tam giác MNE = tam giác MPE (ccc)
=> góc NME = góc PME (2 góc tương ứng)
=> ME là đường phân giác góc NMP (tc)

Xét tam giác MNI và MPI có
MI là cạnh chung
MN = MP( tam giác MNP cân)
Góc MIN = góc MIP = 90°
=> Tam giác MIN = tam giác MIP( cgv - ch)
IN = IP = 5 cm nên I là trung điểm của NP
b) Tam giác MIN vuông tại I có
NI2 + MI2 = MN2( định lí Pytago)
MI2 + 52 = 142
MI2 + 25 = 196
MI2 = 144
MI=12
c) Xét tam giác PHI và PKI có
MI là cạnh chung
Góc HMI = KMI ( tam giác NMI = PMI )
Góc IHM = IKM = 90°
=》 Tam giác HMI = KMI ( ch - gn)
=》IH=IK

a: Xét ΔKNP vuông tại K và ΔHPN vuong tại H có
PN chung
góc KNP=góc HPN
=>ΔKNP=ΔHPN
b: Xét ΔENP có góc ENP=góc EPN
nên ΔENP cân tại E
c: Xét ΔMNE và ΔMPE có
MN=MP
NE=PE
ME chung
=>ΔMNE=ΔMPE
=>góc NME=góc PME
=>ME là phân giác của góc NMP

Bạn tự vẽ hình
`a)`Xét tam giác MNP cân có:MI là trung tuyến
`=>` MI là đường cao
`=>MI bot NP`
`b)` Xét tam giác vuông MIQ và tam giác vuông MIK có:
`MI` chung
`hat{NMI}=hat{PMI}`
`=>DeltaMIQ=DeltaMIK(ch-gn)`
`=>IQ=IK(1)`
`DeltaMIQ=DeltaMIK(ch-gn)`
`=>MQ=MK(2)`
`(1)(2)=>IM` là trung trực QK
Bài khá dài, bạn đọc không hiểu cứ hỏi mình nha!