Cho tam giác ABC. Kẻ AH vuông góc với BC (H ∈ BC). Cho biết AB = 15cm, AH = 12cm, HC = 16cm và góc HAC bằng 37 độ.
a) Tính các độ dài AB và BC.
b) Tính số đo góc ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LA
3 tháng 3 2018
a)\(\Delta ABH\) vuông tại H có:
BH2 =AB2 -AH2 =132 -122 =25( ĐL Pytago)
=> BH=5 cm
BC=BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có:
AH2 + HC2 =AC2 ( đl Pytago)
=> AC2 =122 + 162 =20 cm
b) \(\Delta AHB\) vuông tại H có: AB2 = AH2 +BH2 ( ĐL Pytago)
=> BH2 =AB2 - AH2 =132 - 122 =25
=> BH=5 cm
BC= BH+HC=5+16=21 cm
\(\Delta AHC\) vuông tại H có: AC2 = AH2 +HC2 ( đL Pytago)
=> AC2 = 122 + 162 =400
=> AC= 20 cm
27 tháng 2 2021
Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow AC^2=12^2+16^2=400\)
hay AC=20(cm)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow HB^2=AB^2-AH^2=13^2-12^2=25\)
hay HB=5(cm)
Ta có: HB+HC=BC(H nằm giữa B và C)
nên BC=5+16=21(cm)
Vậy: AC=20cm; BC=21cm
29 tháng 1 2021
AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAC vuông tại H
\(\Rightarrow\) \(^{AC^2}\) = \(^{AH^2}\) + \(^{HC^2}\)
\(\Rightarrow\) \(^{AC^2}\)= \(^{12^2}\) + \(^{16^2}\)
\(\Rightarrow\) \(^{AC^2}\)= 144 + 256
\(\Rightarrow\) \(^{AC^2}\)= 400
\(\Rightarrow\) AC = 20 ( cm )
AH \(\perp\) BC ( gt )
\(\Rightarrow\) Tam giác HAB vuông tại H
\(\Rightarrow\) \(AB^2\) = \(AH^2\) + \(BH^2\)
\(\Rightarrow\) \(BH^2\) = \(AB^2\) - \(AH^2\)
\(\Rightarrow\) \(BH^2\) = \(13^2\) - \(12^2\)
\(\Rightarrow\) \(BH^2\) = 169 - 144
\(\Rightarrow\) \(BH^2\) = 25
\(\Rightarrow\) BH = 5 ( cm )
Có: BH + HC = BC ( Vì H nằm giữa B và C )
\(\Rightarrow\) 5 + 16 = 21 ( cm )
Vậy AC = 20 cm
BC = 21 cm
Học tốt
14 tháng 6 2017
Câu 1:
Xét tam giác ABH vuông tại H, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
202 = AH2 + 162
400 = AH2 + 256
AH2 = 400 - 256
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
AC2 = 122 + 52
AC2 = 144 + 25
AC2 = 169
AC = \(\sqrt{169}\)= 13 (cm)
Vậy AH = 12 cm
AC = 13 cm
Bài 2:
Xét tam giác AHC vuông tại H, ta có:
AC2 = AH2 + HC2 (định lý Py-ta-go)
152 = AH2 + 92
225 = AH2 + 81
AH2 = 225 - 81
AH2 = 144
AH = \(\sqrt{144}\)= 12 (cm)
Xét tam giác AHB vuông tại, ta có:
AB2 = AH2 + HB2 (định lý Py-ta-go)
AB2 = 122 + 52
AB2 = 144 + 25
AB2 = 169
AB = \(\sqrt{169}\)= 13 (cm)
Vậy AB = 13 cm
CM
31 tháng 3 2018
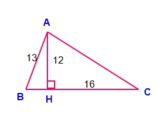
Áp dụng định lí Pi-ta-go trong ΔAHC vuông tại H ta có:
AC2 = AH2 + HC2 = 122 + 162 = 144 + 256 = 400
⇒ AC = 20 (cm)
Áp dụng định lí Pi-ta-go trong ΔAHB vuông tại H ta có:
BH2 + AH2 = AB2 ⇒ BH2 = AB2 - AH2 = 132 - 122 = 169 -144 = 25
⇒ BH = 5cm
Do đó BC = BH + HC = 5 + 16 = 21 (cm)
1 tháng 4 2020
Trả lời :
Bạn vào câu hỏi tương tự hoặc lên mạng kham khải bài nhá.
# chúc bạn học tốt ạ #
P/s bạn kia làm cái gì mà mình không hiểu
a) có AB = 15cm ( bài cho)
Xét tam giác AHC có góc AHC = 90 độ( AH vuông góc với BC)
theo định lý py-ta-go có
AB^2= AH^2+BH^2
=> BH^2 = AB^2 - AH^2
=> BH^2= 15^2- 12^2= 81
=> BH= 9
có BH+ HC=BC => BC= 9+16= 25
Vậy ta có AB= 15cm; BC= 25cm
câu sau tương tự bạn đó ( câu đầu làm mình không thấy tính AB với BC đâu hết )
a)Ta có: \(AC^2=AH^2+HC^2\)(định lý pytago)
\(\Rightarrow AC^2=12^2+16^2=144+256=400\)
\(\Rightarrow AC=20cm\)
b)Ta có:\(\widehat{HAC}\)\(+\)\(\widehat{AHC}\)\(+\)\(\widehat{ACH}\)\(=180^o\)(tổng 3 góc trong 1 tam giác)
\(\Rightarrow\widehat{ACH}\)\(=180^o\)\(-\widehat{HAC}\)\(-\widehat{AHC}\)\(=180^o\)\(-37^o-90^o=53^o\)
ta có:\(\widehat{ABC}\)\(=\widehat{HAC}\)\(+\widehat{ACH}\)(tính chất góc ngoài của tam giác)
Hay:\(\widehat{ABC}\)\(=37^o+53^o=90^o\)