cho nửa đường tròn tâm o đường kính ab cố định. gọi c là điểm chính giữa của cung ab và m là điểm bất kì thuộc cung ac. bm cắt oc tại d. tiếp tuyến với nửa đường tròn tâm o tại điểm m cắt đường cd tại điểm e.
Cm:a)bd,bm ko có giá trị phụ thuộc vào vị trí điểm m
b)ed=em.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
11 tháng 7 2021
AB cắt đường tròn ngoại tiếp tam giác AEK tại D
Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle EMB+\angle EHB=90+90=180\)
\(\Rightarrow EMBH\) nội tiếp \(\Rightarrow\angle KBD=\angle MBH=\angle AEH\)
Vì KEAD nội tiếp \(\Rightarrow\angle AEH=\angle KDB\Rightarrow\angle KBD=\angle KDB\)
\(\Rightarrow\Delta KDB\) cân tại K có KH là đường cao
\(\Rightarrow H\) là trung điểm BD mà B,H cố định \(\Rightarrow D\) cố định
Vì KEAD nội tiếp \(\Rightarrow I\in\) trung trực AD mà A,D cố định
\(\Rightarrow\) đpcm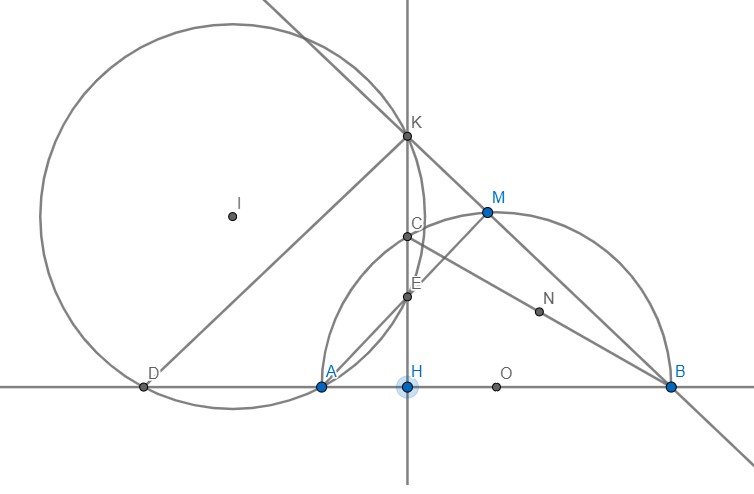
3 tháng 7 2023
a: C là điểm chính giữa của cung AB
=>OC vuông góc AB
góc OHE=góc OME=90 độ
=>OHME nội tiếp
b: góc AMB=1/2*sđ cung AB=90 độ
=>góc AMH+góc AOH=180 độ
=>OHMA nội tiếp
=>O,H,M,E,A cùng thuộc 1 đường tròn
=>góc EAO=90 độ
OHEA có 3 góc vuông
=>OHEA là hcn
=>EH=OA=R
14 tháng 7 2019
Gọi BE cắt đường tròn (O) tại điểm thứ hai là N. Gọi L là hình chiếu của I trên ME.
Dễ thấy ^BNA = 900. Suy ra \(\Delta\)BNA ~ \(\Delta\)BCE (g.g) => BN.BE = BC.BA
Cũng dễ có \(\Delta\)BMA ~ \(\Delta\)BCK (g.g) => BC.BA = BM.BK. Do đó BN.BE = BM.BK
Suy ra tứ giác KENM nội tiếp. Từ đây ta có biến đổi góc: ^KNA = 3600 - ^ANM - ^KNM
= (1800 - ^ANM) + (1800 - ^KNM) = ^ABM + (1800 - ^AEM) = ^EFM + ^MEF = ^KFA
=> 4 điểm A,K,N,F cùng thuộc một đường tròn. Nói cách khác, đường tròn (I) cắt (O) tại N khác A
=> OI vuông góc AN. Mà AN cũng vuông góc BE nên BE // OI (1)
Mặt khác dễ có E là trung điểm dây KF của (I) => IE vuông góc KF => IE // AB (2)
Từ (1);(2) suy ra BOIE là hình bình hành => IE = OB = const
Ta lại có EM,AB cố định => Góc hợp bởi EM và AB không đổi. Vì IE // AB nên ^IEL không đổi
=> Sin^IEL = const hay \(\frac{IL}{IE}=const\). Mà IE không đổi (cmt) nên IL cũng không đổi
Vậy I di động trên đường thẳng cố định song song với ME, cách ME một khoảng không đổi (đpcm).
26 tháng 3 2021
a) Xét (O) có
\(\widehat{AMB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AMB}=90^0\)(Hệ quả góc nội tiếp)
hay \(\widehat{FMB}=90^0\)
Xét tứ giác BCFM có
\(\widehat{FCB}\) và \(\widehat{FMB}\) là hai góc đối
\(\widehat{FCB}+\widehat{FMB}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: BCFM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
a.tứ giác AMDO nội tiếp (∠AOD+∠AMD=180)
⇒BD.BM=BO.BA
mà A,B,O cố định nên BO.BA không đổi
⇒BD.BM không có giá trị phụ thuộc vào vị trí điểm m
b.có ∠EMB=\(\dfrac{1}{2}\stackrel\frown{MB}\) (góc tạo bởi tia tiếp tuyến và dây cung)
do tứ giác AMDO nội tiếp⇒∠MAO=∠MDE(1)
∠MAO=\(\dfrac{1}{2}\stackrel\frown{MB}\)
⇒∠EMB=∠MAO(2)
từ (1) và (2) ⇒∠EMB=∠MDE
⇒ΔEMD cân tại E
⇒ED=EM