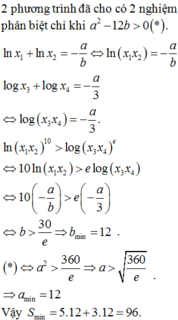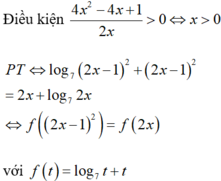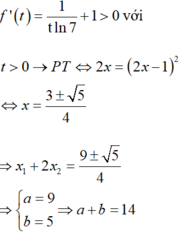Cho phương trình x2+ ax + b=0 có hai nghiệm nguyên dương biết a,b là hai số thõa mãn 5a + b=22.Tìm hai nghiệm đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
28 tháng 2 2016
Ta có:
- \(x^2+y^2+x+y=4\)
- x(x+y+1)+y(y+1)=2
=>
- x^2+y^2+x+y=4
- x^2+y^2+x+y+xy=2
=>
- (x+y)^2+(x+y)-2xy=4
- xy=-2
=>
- (x+y)(x+y+1)=0
- xy=-2
=>1)
- x+y=0
- xy=-2
2)
- x+y=-1
- xy=-2
giải các hệ pt 1) và 2) ta được (x;y)=(\(\left(\sqrt{2};-\sqrt{2}\right),\left(-\sqrt{2};\sqrt{2}\right),\left(-2;1\right),\left(1;-2\right)\)
29 tháng 10 2023
a: Khi m=1 thì phương trình sẽ là:
\(x^2-2x+1-1=0\)
=>x^2-2x=0
=>x(x-2)=0
=>x=0 hoặc x=2
b: \(\text{Δ}=\left(-2\right)^2-4\left(m-1\right)=4-4m+4=-4m+8\)
Để phương trình có 2 nghiệm thì -4m+8>=0
=>-4m>=-8
=>m<=2
\(x_1^3+x_2^3< =15\)
=>\(\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)< =15\)
=>\(2^3-3\cdot2\cdot\left(m-1\right)< =15\)
=>\(8-6m+6< =15\)
=>-6m+14<=15
=>-6m<=1
=>\(m>=-\dfrac{1}{6}\)
=>\(-\dfrac{1}{6}< =m< =2\)
19 tháng 5 2020
Theo hệ thức Vi-et ta có \(\left\{{}\begin{matrix}x_1+x_2=-a\\x_1x_2=b\end{matrix}\right.\)
\(\Rightarrow5a+b=22\)
\(\Leftrightarrow x_1x_2-5\left(x_1+x_2\right)=22\)
\(\Leftrightarrow\left(x_1-5\right)\left(x_2-5\right)=47\)
Vì x1,x2 là số nguyên dương nên
\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x_1-5=1\\x_2-5=47\end{matrix}\right.\\\left\{{}\begin{matrix}x_1-5=47\\x_2-5=1\end{matrix}\right.\end{matrix}\right.\)=>.....
CM
4 tháng 2 2019
Đáp án C
Điều kiện 4 x 2 − 4 x + 1 2 x > 0 ⇔ x > 0
P T ⇔ log 7 2 x − 1 2 + 2 x − 1 2 = 2 x + log 7 2 x ⇔ f 2 x − 1 2 = f 2 x
với f t = log 7 t + t
f ' t = 1 t ln 7 + 1 > 0 với t >0
→ P T ⇔ 2 x = 2 x − 1 2 ⇔ x = 3 ± 5 4
⇒ x 1 + 2 x 2 = 9 ± 5 4 ⇒ a = 9 b = 5 ⇒ a + b = 14
1 tháng 2 2022
Ý bạn ấy là \(x_1^2\)nhưng bạn ấy chưa biết chỗ để đánh chỉ số dưới. Bạn nhấn vào cái biểu tượng x2 ở chỗ khung điều chỉnh thì con trỏ hạ xuống để bạn gõ chỉ số dưới. Xong rồi thì nhấn vào biểu tượng đó lần nữa.