Cho các điểm A(a;0;0) B(0;b;0) C( 0;0;c) trong đó a,b,c>0, a^2+b^2+c^2=3. Tìm giá trị lớn nhất của khoảng cách từ gốc toạ độ O đến mặt phẳng (ABC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 7 2018
a) Xác định các điểm –a, -b trên trục số:
b) Xác định các điểm |a|, |b|, |-a|, |-b| trên trục số:
c) So sánh các số a, b, -a, -b, |a|, |b|, |-a|, |-b| với 0:
a ở bên trái trục số ⇒ a là số nguyên âm nên a < 0.
Do đó: -a = |-a| = |a| > 0.
b ở bên phải trục số ⇒ b là số nguyên dương nên b = |b| = |-b| > 0 và -b < 0.
8 tháng 6 2017
a) Hình :
Khi đó có :
- Các tia : AB,AC,BA,BC,CA,CB;
- Các tia sau đây là đối nhau : BA và BC
- Các tia sau đây là phân biệt : AB và BC ; AC và BC ; BA và BC ; CA và BA ; CB và BA ; AC và CA ;BC và CB.
- Các cặp tia sau là trùng nhau : AB và AC ; CA và CB.
b) làm giống ý a.
CM
23 tháng 7 2017
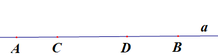
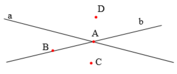
a) Trên hình có các đường thẳng: đường thẳng a; đường thẳng b.
b) Trên hình có các điểm: Điểm A; điểm B; điểm C; điểm D;
c) Điểm A thuộc đường thẳng a; Còn các điểm B; điểm C; điểm D không thuộc đường thẳng a.
d) Điểm A và điểm B thuộc đường thẳng b; Còn các điểm C; điểm D không thuộc đường thẳng b.
CM
19 tháng 10 2019
a) Điểm A nằm giữa hai điểm C và B.
b) Điểm B và D nằm khác phía đối với điểm A. Điểm C và D năm khác phía đối với điểm A.
CM
12 tháng 11 2017
Các tam giác trên có hai loại:
+ Loại 1: Gồm các tam giác có 2 đỉnh điểm nằm trên a, 1 đỉnh nằm trên b. Số tam giác thuộc loại này là 
+ Loại 2: Gồm các tam giác có 1 đỉnh điểm nằm trên a, 2 đỉnh nằm trên b. Số tam giác thuộc loại này là 
Vậy theo quy tắc cộng, số tam giác cân tìm là: 120 + 168 = 288.
Chọn C.
CM
25 tháng 3 2018
a/ Điểm B và D nằm cùng phía đối với điểm C;
Điểm A và D, A và B nằm khác phía đối với C
b/ CA và CD, CA và CB đối nhau; CB và CD trùng nhau
c/ Ta có: Điểm D nằm giữa B, C nên D ∈ CB (1)
Điểm C nằm giữa A, B nên hai tia CA, CB đối nhau (2)
Từ (1),(2) => CA, CD là hai tia đối nhau => C nằm giữa A, D.
1 tháng 2
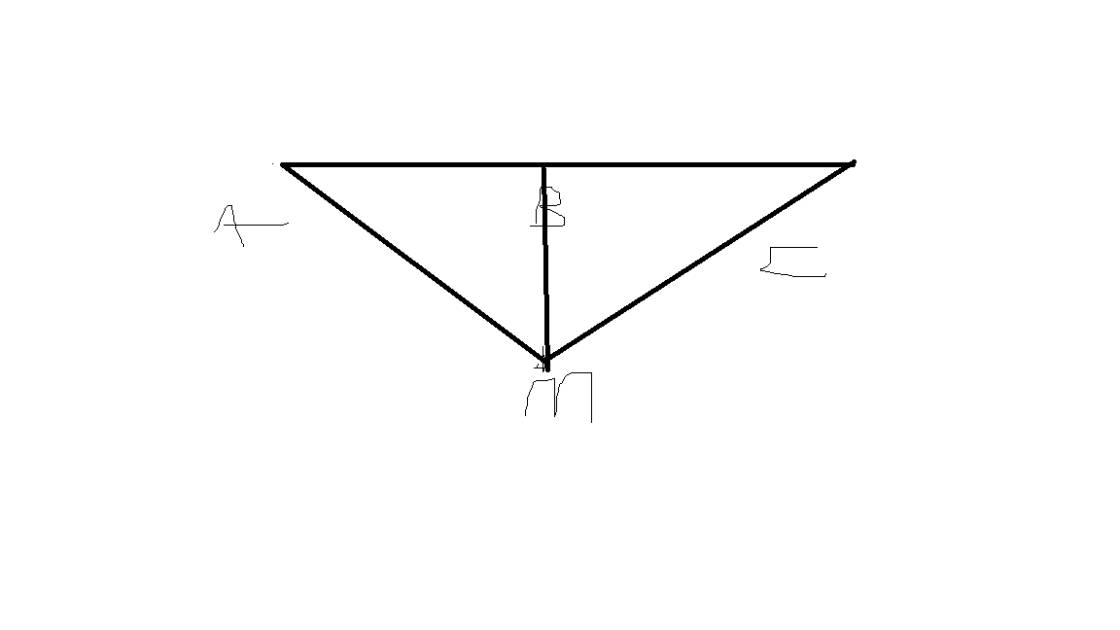
Bài 1:
a: Vì B nằm giữa A và C
nên tia BA và tia BC là hai tia đối nhau
mà D thuộc tia BA(D nằm giữa B và A)
nên BD và BC là hai tia đối nhau
=>B nằm giữa D và C
b: Các tia đối nhau là:
BA và BC
BD và BC
DA và DC
DA và DB
c: Các tia trùng nhau là AD,AB,AC; DB;DC
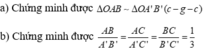
\(\left(ABC\right):\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)
\(d\left[O,\left(ABC\right)\right]=\dfrac{1}{\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}}\)
\(d_{max}\Rightarrow\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\right)_{min}\)
Theo cô si: \(a^2+b^2+c^2\ge3\sqrt[3]{a^2b^2c^2}\Leftrightarrow3\ge3\sqrt[3]{a^2b^2c^2}\Rightarrow a^2b^2c^2\le1\) \(\Leftrightarrow\dfrac{1}{a^2b^2c^2}\ge1\)
Và: \(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge3\sqrt[3]{\dfrac{1}{a^2}\dfrac{1}{b^2}.\dfrac{1}{c^2}}\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}\ge3\)
Dấu "=" xảy ra khi \(\dfrac{1}{a^2}=\dfrac{1}{b^2}=\dfrac{1}{c^2}\Leftrightarrow a=b=c=1\)
\(\Rightarrow d_{max}=\dfrac{\sqrt{3}}{3}\)