Cho hai vecto a;b khác vecto 0 thỏa mãn \(\overrightarrow{a}.\overrightarrow{b}=\dfrac{1}{2}\left|-\overrightarrow{a}\right|\left|\overrightarrow{b}\right|\). Khi đó góc giữa hai vecto a và b là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{\left(-1\right)\cdot2+1\cdot0}{\sqrt{\left(-1\right)^2+1^2}+\sqrt{2^2+0^2}}=-2+\sqrt{2}\)
\(\Leftrightarrow\left(\overrightarrow{a},\overrightarrow{b}\right)=125^0\)

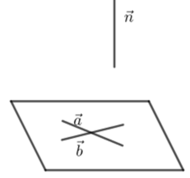
Phương án A và C sai vì có thể xảy ra trường hợp như hình vẽ sau
Giả sử phương án B cũng sai, tức là ba vecto n → , a → v à b → đồng phẳng. Khi đó vì n→ ⊥ a→ và n→ ⊥ b→ nên giá của a → v à b → song song. Điều này mẫu thuẫn với giả thiết hai vecto a → v à b → không cùng phương. Vì vậy phương án B đúng.
Đáp án B

Ta có: \(\dfrac{-3}{1}\ne\dfrac{0}{2}\Rightarrow\overrightarrow{a}\) và \(\overrightarrow{b}\) ko cùng phương
b. Đặt \(\overrightarrow{c}=x.\overrightarrow{a}+y.\overrightarrow{b}\)
\(\Rightarrow\left(-1;3\right)=x.\left(1;2\right)+y.\left(-3;0\right)=\left(x-3y;2x\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x-3y=-1\\2x=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{5}{6}\end{matrix}\right.\)
\(\Rightarrow\overrightarrow{c}=\dfrac{3}{2}\overrightarrow{a}+\dfrac{5}{6}\overrightarrow{b}\)

\(cos\left(\overrightarrow{a},\overrightarrow{b}\right)=\dfrac{1\cdot\left(-1\right)+\left(-2\right)\cdot\left(-3\right)}{\sqrt{1^2+2^2}\cdot\sqrt{1^2+3^2}}=\dfrac{5}{\sqrt{5}\cdot\sqrt{10}}=\dfrac{5}{\sqrt{50}}=\dfrac{1}{\sqrt{2}}\)

a) Gọi M, N lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Vì \(\overrightarrow a = \overrightarrow {AB} \Leftrightarrow \overrightarrow {MN} = \overrightarrow {AB} \) nên tứ giác MNBA là hình bình hành.
Nói cách khác B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \) và điểm A.
Tương tự, C là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \) và điểm B.
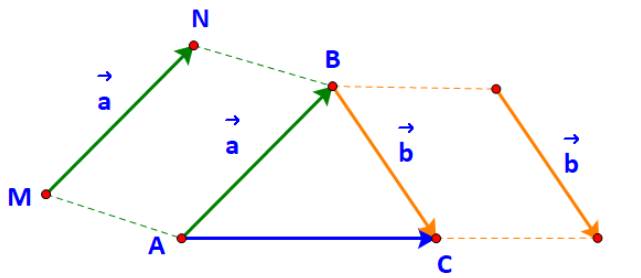
b) Dễ thấy: tổng của hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {BC} \) là vecto \(\overrightarrow {AC} \).
Do đó tổng của hai vecto \(\overrightarrow a \) và \(\overrightarrow b \)bằng vecto \(\overrightarrow {AC} \).
Ta có viết: \(\overrightarrow a + \overrightarrow b = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)

Đẳng thức đúng khi và chỉ khi \(\overrightarrow{a}.\overrightarrow{b}=0\) hay \(\overrightarrow{a}\perp\overrightarrow{b}\) hoặc 1 trong 2 vecto là vecto - không

Phương án A sai vì có thể xảy ra trường hợp giống câu 4 như hình sau:

Phương án B và C sai vì có thể sảy ra như hình sau.

Phương án D đúng vì: có thể ba vecto n → , a → , b → đồng phẳng hoặc không đồng phẳng như hai hình trên.
Đáp án D
Giả thiết => cos \(\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{1}{2}\)
⇒ \(\left(\overrightarrow{a};\overrightarrow{b}\right)=60^0\)