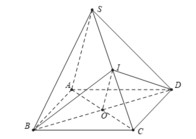
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O, SA=SC; SB=SD. Trong các khẳng định sau, khẳng định nào đúng?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Xét tam giác SAC có SA = SC \( \Rightarrow \) SAC là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) AC.
Xét tam giác SBD có SB = SD \( \Rightarrow \) SBD là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) BD.
+) Ta có SO \( \bot \) AC; SO \( \bot \) BD; AC \( \cap \) BD tại O \( \Rightarrow \) SO \( \bot \) (ABCD).

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

Chọn C.
+) Ta có:
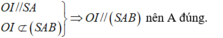
+) Ta có:
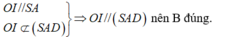
+) Ta có: mp (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai.
+) Ta có: (IBD) ∩ (SAC) = IO nên D đúng.

Đáp án C
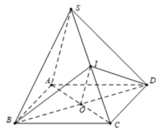
Ta có: O I / / S A O I ∉ S A B ⇒ O I / / S A B nên A đúng
Ta có: O I / / S A O I ∉ S A D ⇒ O I / / S A D nên B đúng
Ta có: (IBD)cắt hình chóp theo thiết diện là tam giác IBD nên
Ta có: I B D ∩ S A C = I O nên D đúng.

Chọn B.
Phương pháp: Xét tính đúng sai của từng mệnh đề.
Cách giải: B sai vì mặt phẳng (IBD) cắt hình chóp S.ABCD theo thiết diện là ∆ I B D

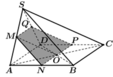
Tham khảo hình vẽ bên.
Gọi P, Q lần lượt là trung điểm của CD, SD. Khi đó thiết diện tạo bởi mặt phẳng (OMN) với hình chóp là hình thang MNPQ. Thật vậy:
![]()
Chọn B.

\(SM=MA=SA-SM\Rightarrow SM=\dfrac{1}{2}SA\)
Do IM song song SO, áp dụng định lý Talet trong tam giác SAO:
\(\dfrac{IO}{OA}=\dfrac{SM}{SA}=\dfrac{1}{2}\)
Do NK song song SO, áp dụng định lý Talet cho tam giác SCO:
\(\dfrac{OK}{OC}=\dfrac{SN}{SC}=\dfrac{1}{3}\)
Mà ABCD là hình bình hành nên \(OA=OC\)
\(\Rightarrow\dfrac{OI}{OK}=\dfrac{3}{2}\)
ĐÁP ÁN: B