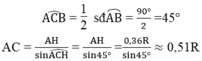Giải bài toán hình Cho tam giác ABC đều nội tiếp trong (O;R) . Trên cạnh AB và AC lấy hai điểm M,N sao cho BM= AN . 1 Chứng tỏ tam giác OMN cân 2 Chứng minh tứ giác OMAN nội tiếp 3 BO kéo dài cắt AC tại D và cắt (O) tại E.Chứng minh BD^2+DC^2=3R^2 4 Đường thẳng CE và AB cắt nhau tại F. Tiếp tuyến tại A của (O) cắt FC tại I;AO kéo dài cắt BC tại J.Chứng minh BI đi qua trung điểm của AJ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 3 2023
a: góc OAD+góc OBD=180 độ
=>OADB nội tiếp
b: góc OAB+góc OBA=1/2*120=60 độ
=>góc AOB=120 độ
=>góc ADB=60 độ
=>CA=AD=DB=CB
=>CADB là hình thoi
CM
14 tháng 11 2018
Chọn đáp án C.
Gọi M là trung điểm của BC: 
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:
CM
26 tháng 6 2019
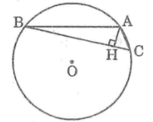
Dây AB bằng cạnh hình vuông nội tiếp đường tròn (O) nên ta có: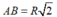 
và cung nhỏ AB có số đo bằng
360
°
:
4
=
90
°
Dây BC bằng cạnh hình tam giác đều nội tiếp đường tròn (O) nên ta có:
BC = R 3 và cung nhỏ BC có số đo bằng 360 ° : 3 = 120 °
Ta có:
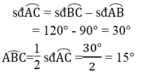
Trong tam giác vuông ABH ta có:
Trong tam giác vuông ACH ta có:
