Thay \(AB;CD;EF;PQ\) độ dài , ta được
\(\dfrac{AB}{CD}=\dfrac{6}{7}\)
\(\dfrac{EF}{PQ}=\dfrac{18}{21}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a= 4 hoăc 3
b= 3 howacj 4 hiểu chư
thay 34+ 43 hoặc
43 + 34
TA có 11 x (a+b)=77 nên a+b=7 suy ra (a,b)=(1,6)(2,7)(3,4)(5,2)(6,1)(0,7),(7,0)

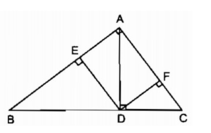
DE và CA cùng vuông góc với AB, do đó
DE // AC.
Theo định lí Ta-lét, ta có:
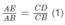
Tương tự, ta có: DF // AB, do đó:
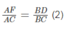
Cộng các vế tương ứng của (1) và (2), ta có:
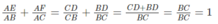
Tổng 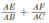 không thay đổi vì luôn có giá trị bằng 1.
không thay đổi vì luôn có giá trị bằng 1.
Vậy : Khi độ dài cạnh góc vuông AB, AC của tam giác vuông ABC thay đổi thì tổng 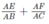 luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.
luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng 1.


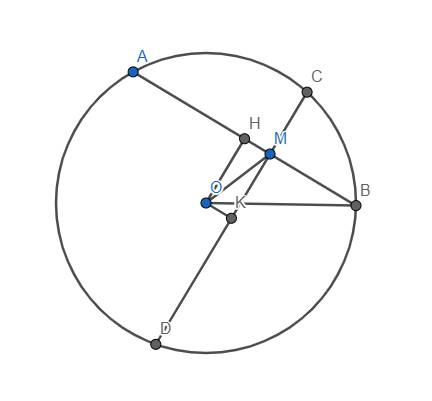
Hạ \(OH\perp AB\), \(OK\perp CD\). Dễ thấy tứ giác OHMK là hình chữ nhật \(\Rightarrow HK=OM\)
Lại có \(AB^2=4HB^2=4\left(OB^2-OH^2\right)=4R^2-4OH^2\) (1)
và \(CD^2=4CK^2=4\left(OC^2-OK^2\right)=4R^2-4OK^2\) (2)
Từ (1) và (2), suy ra \(AB^2+CD^2=8R^2-4\left(OH^2+OK^2\right)\) \(=8R^2-4HK^2=8R^2-4OM^2\) không đổi, đpcm.

A B D C M K H F E
xét tg AMCH có: E là t/đ của của MH và AC => tg AMCH là hbh=> AM//HC
xét tg BMDK có: F là t/đ của MK và BD => tg BMDK là hbh => BM//DK
Mà M thuộc AB (gt) => AB // HC//DK. (1)
Mặt khác : AB // DC (2)
Từ (1),(2)=> D,K,H,C thẳng hàng (tiên đề Ơ -clit)
b) do tg AMCH là hbh (c/m câu a)=> AM=CH (3)
Do tg BMDK là hbh (.................)=> BM=DK (4)
Từ(3),(4)=> AM+BM=CH+DK
=> AB=CH+DK (5)
Mặt khác: Dk+KH+HC=DC=> KH=DC-(DK+HC) (6)
Từ (5),(6),=> HK=DC-AB
Mà hthang ABCD cố định nên AB và DC ko đổi => DC-AB ko đổi => HK ko đổi
Vậy khi M di chuyển trên AB thì độ dài HK ko đổi
ròi kêu lmj?
Đề ??