Cho tam giác MAB cân tại M. Kẻ MI là tia phân giác của góc M (I ϵ AB)
Tưd I kẻ IH vuông góc MA ( H ϵ AM); IK vuông góc MB (K ϵ MB). Chứng minh rằng:
a) tam giác MIH = tam giác MIK
b) IH = IK
c) tam giác MHK cân tại M
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=10^2-6^2=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
b: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>\(\widehat{BAH}=\widehat{CAH}\)
=>AH là phân giác của góc BAC
c: Ta có: ΔAHB=ΔAHC
=>BH=CH
Xét ΔBMH vuông tại M và ΔCNH vuông tại N có
BH=CH
\(\widehat{B}=\widehat{C}\)
Do đó: ΔBMH=ΔCNH
d: Xét ΔABO vuông tại B và ΔACO vuông tại C có
AO chung
AB=AC
Do đó: ΔABO=ΔACO
=>OB=OC
=>ΔOBC cân tại O

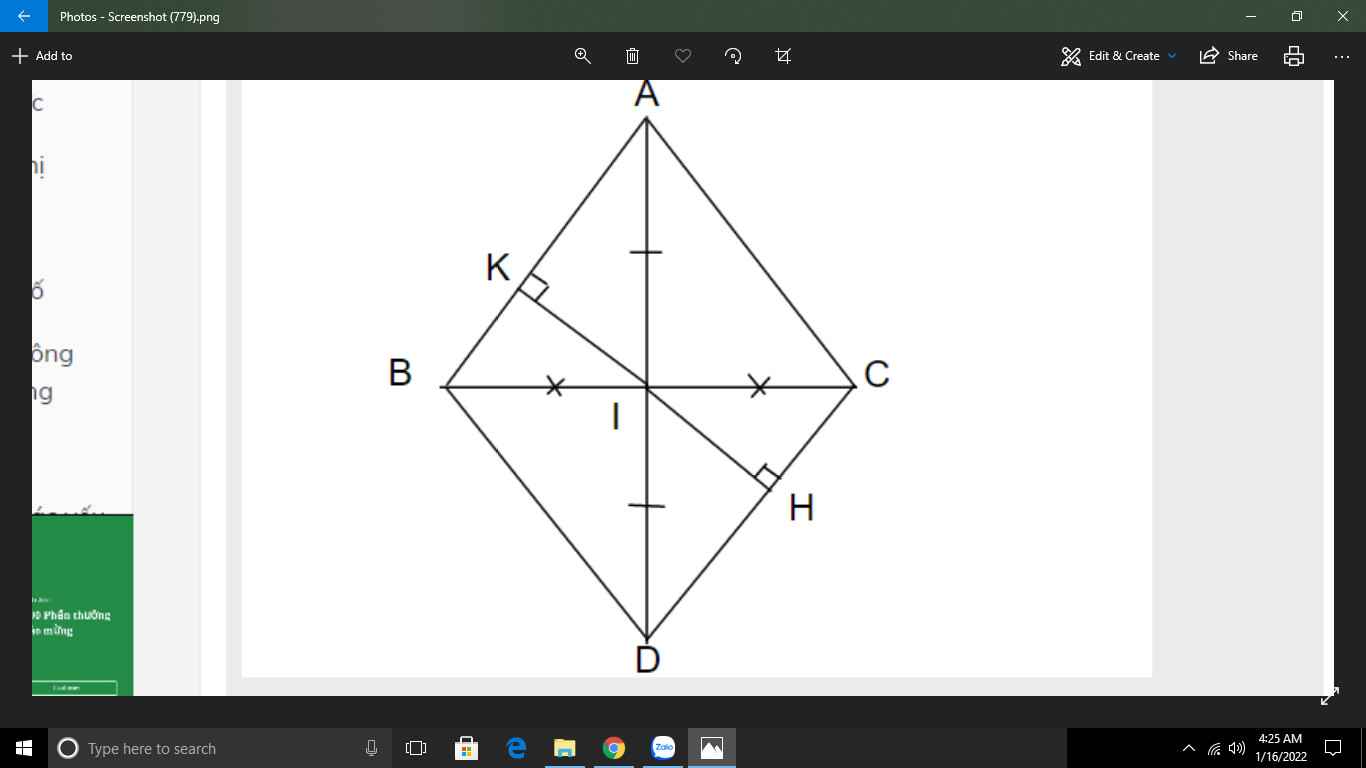
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)

a: Xét ΔMAE và ΔMBE có
MA=MB
\(\widehat{AME}=\widehat{BME}\)
ME chung
Do đó: ΔMAE=ΔMBE
b: Xét ΔMHE vuông tại H và ΔMKE vuông tại K có
ME chung
\(\widehat{HME}=\widehat{KME}\)
Do đó:ΔMHE=ΔMKE
Suy ra: EH=EK
c: Ta có: ΔMAB cân tại M
mà ME là đường trung tuyến
nên ME là đường cao
=>ΔEBI vuông tại E

a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
=>AB=DC
b: Xét ΔMAC và ΔMDB có
MA=MD
\(\widehat{AMC}=\widehat{DMB}\)
MC=MB
Do đó: ΔMAC=ΔMDB
=>\(\widehat{MAC}=\widehat{MDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên BD//AC

Xét ΔDEI vuông tại E và ΔDHI vuông tại H có
DI chung
góc EDI=góc HDI
=>ΔDEI=ΔDHI
a, Ta có △MAB cân tại M => AM=BM(đ/l)=>MI là đường trung trực của AB
=>AI=IB(t/c)
=> góc MAB = góc MBA (đ/l)
Ta có IH vuông góc với AM=> góc IHA=90 độ
Ta có IK vuông góc với MB=> góc IKB = 90 độ
Xét △AHI và △ IBK ta có:
Góc IHA= góc IKB=90 độ(CMT) \
AI=IB(CMT) => △AHI =△ IBK ( cạnh huyền - góc gócMAB=gócMBA(CMT) / nhọn)
b, => IH=IK (2 cạnh tương ứng); => AH=KB (2 cạnh tương ứng)
c, Ta có AM= HM+AH (1)
BM=KM+IK (2)
mà AM=BM (CMT); AH=IK(CMT) (3)
Từ (1), (2), (3) => HM = MK (t/c)
=> △ MHK cân tại M (t/c)
vẽ hình ra í ạ