Cho tứ giác ABCD nội tiếp đường tròn (O). Biết hai đường chéo AC,BD vuông góc với nhau và AB=12;CD=4. Diện tích hình tròn (O) bằng
A.80\(\pi\)
B.\(4\pi\sqrt{10}\)
C.\(40\pi\)
D.\(20\pi\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 6 2017
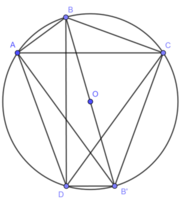
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: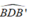
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do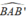 
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)
CH
Cô Hoàng Huyền
Admin
VIP
18 tháng 5 2016
Cô hướng dẫn nhé. :)
Tứ giác AIDE nội tiếp đường tròn đường kính AI.
b. Do câu a ta có AIDE là tứ giác nội tiếp nên gó IDE = góc IAE. Lại có góc IAE = góc CDB. Từ đó suy ra DB là tia phân giac góc CDE.
c. Ta thấy góc CDE = 2 góc CAB (Chứng minh b). Lại có góc COB = 2 góc CAB. Từ đó suy ra góc CDE = góc COB. Hay OEDC là tứ giác nội tiếp ( Góc ngoài ở đỉnh bằng góc đối diện )
Chúc em học tốt ^^
22 tháng 3 2021
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
19 tháng 3 2020
Tự vẽ hình nha ><
a) ^ABD = 900 => ^ABE = 900
EF \(\perp\)AD => ^EFA = 900
=> Tứ giác ABEF có tổng 2 góc đối = 900 nội tiếp được đường tròn