cho tam giác ABC vuông tại A ,ABC=60 độ;BD là Phân giác của ABC. ( D thuộc AC). Kẻ DE vuông góc BC ( E thuộc BC)
a. biết BC = 10cm AB=5 cm tính cạnh AC? b. so sánh: DE và DC
c chứng minh tg ABD = tg EBD
d chứng minh tg BDC cân
e kẻ CF vuông góc BD ( F thuộc tia BD) chứng minh BA;ED và CF đồng quy
GIÚP MIK VỚI Ạ MIK CẦN RẤT GẤP

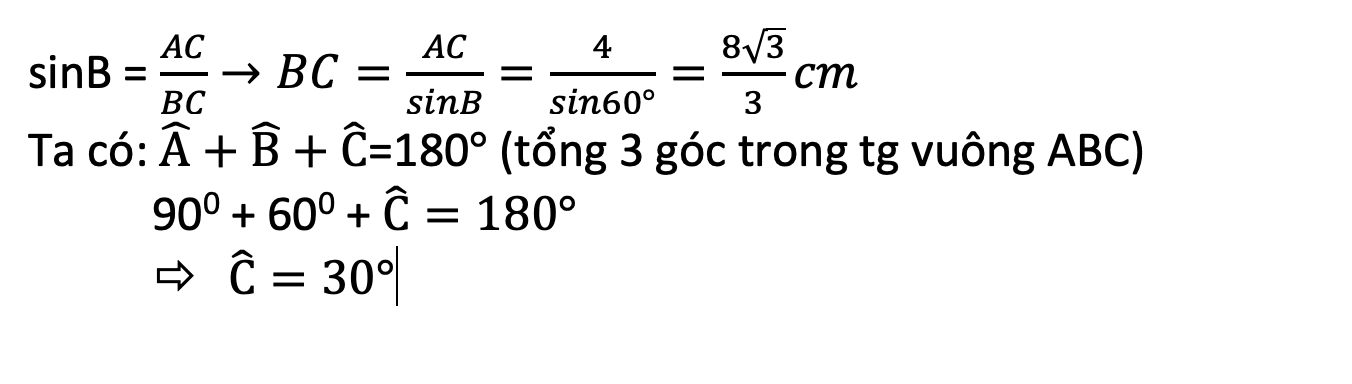

a: \(AC=\sqrt{10^2-5^2}=5\sqrt{3}\left(cm\right)\)
b: ΔDEC vuông tại E
=>DE<DC
c: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
d: Xét ΔDBC có góc DBC=góc DCB
nên ΔDBC cân tại D
e: gọi giao của CF và AB là H
Xét ΔBHC có
BF,CA là đường cao
BF cắt CA tại D
=>D là trực tâm
=>HD vuông góc BC tại E
=>H,D,E thẳng hàng
=>BA,DE,CF là trực tâm