33. Có bao nhiêu số nguyên m thuộc (-2018;2018) để đồ thị hs y = \(\dfrac{x^3+m}{x^3+mx}\) có 4 đường tiệm cận.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hàm số bậc nhất đồng biến suy ra a > 0 hay m > 2
m thuộc đoạn [-2018; 2018] suy ra m thuộc {3; 4; ...; 2018}
Vậy có 2016 giá trị nguyên của m cần tìm.
Chọn D.

Chọn B
Phương pháp: Sử dụng đạo hàm của hàm hợp để tính đạo hàm.


Đáp án A.
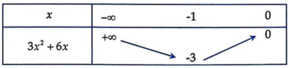
Ta có y ' = − 3 x 2 − 6 x + 4 m =>Hàm số nghịch biến trên − ∞ ; 0
⇔ y ' ≤ 0 ∀ x ∈ − ∞ ; 0 ⇔ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0
Bảng biến thiên:
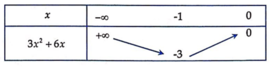
⇒ 3 x 2 + 6 x ≥ − 3 ∀ x ∈ − ∞ ; 0 ⇒ 4 m ≤ 3 x 2 + 6 x ∀ x ∈ − ∞ ; 0
⇔ 4 m ≤ − 3 ⇔ m ≤ − 3 4 ⇒ m ∈ − 2018 ; − 3 4 m ∈ ℤ

Đáp án D
Cách giải:
![]()
![]()
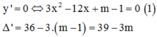
+ ![]() => Hàm số đồng biến trên
=> Hàm số đồng biến trên ![]()
+ ![]() Phương trình (1) có 2 nghiệm phân biệt
Phương trình (1) có 2 nghiệm phân biệt ![]()
Theo đinh lí Viet ta có 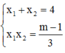
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
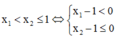
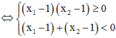
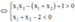
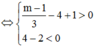 ( vô lí )
( vô lí )
Vậy m ≥ 13
Mà ![]()
![]()
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006



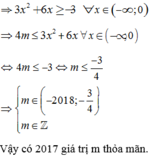
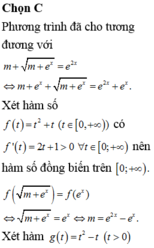


Đề không nói tiệm cận đứng/ ngang/ xiên à bạn?
Bậc tử bằng bậc mẫu nên ĐTHS không có tiệm cận xiên
\(\lim\limits_{x\rightarrow\infty}\dfrac{x^3+m}{x^3+mx}=\lim\limits_{x\rightarrow\infty}\dfrac{1+\dfrac{m}{x^3}}{1+\dfrac{m}{x^2}}=1\)
\(\Rightarrow y=1\) là tiệm cận ngang
ĐTHS có 4 tiệm cận khi nó có 3 TCĐ
\(x^3+m=0\Rightarrow x=-\sqrt[3]{m}\)
\(x^3+mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=-m\end{matrix}\right.\)
\(\Rightarrow\)Hàm có 3 TCĐ khi \(m>0\)