Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m+3\right)x-5}{x+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m+3\right)x-5}{x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{2m+3-\dfrac{5}{x}}{1+\dfrac{1}{x}}=2m+3\)
=>Đường thẳng y=2m+3 là đường tiệm cận ngang duy nhất của đồ thị hàm số \(y=\dfrac{\left(2m+3\right)x-5}{x+1}\)
Để đường thẳng y=2m+3 đi qua A(-1;3) thì 2m+3=3
=>2m=0
=>m=0
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m^2-3m-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=m^2-3m\)
=>Đường thẳng \(y=m^2-3m\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m^2-3m\right)x^2-1}{x^2+1}\)
=>\(m^2-3m=-2\)
=>\(m^2-3m+2=0\)
=>(m-1)(m-2)=0
=>m=1 hoặc m=2
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow+\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{mx-1}{2x+m}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-\dfrac{1}{x}}{2+\dfrac{m}{x}}=\dfrac{m}{2}\)
Vậy: x=m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{mx-1}{2x+m}\)
Để x=m/2 đi qua \(A\left(-1;\sqrt{2}\right)\) thì \(\dfrac{m}{2}=-1\)
=>\(m=-1\cdot2=-2\)
b: \(\lim\limits_{x\rightarrow-\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow-\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x-2}{2x-m}=\lim\limits_{x\rightarrow+\infty}\dfrac{1-\dfrac{2}{x}}{2-\dfrac{m}{x}}=\dfrac{1}{2}\)
=>x=1/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
=>Không có giá trị nào của m để đường thẳng x=1 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x-2}{2x-m}\)
a: \(\lim\limits_{x\rightarrow-\dfrac{3m}{2}}\dfrac{x+3}{2x+3m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-\dfrac{3m}{2}}2x+3m=0\\\lim\limits_{x\rightarrow-\dfrac{3m}{2}}x+3=\dfrac{-3m}{2}+3\end{matrix}\right.\)
=>x=-3m/2 là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\)
Để tiệm cận đứng của đồ thị hàm số \(y=\dfrac{x+3}{2x+3m}\) đi qua M(3;-1) thì \(-\dfrac{3m}{2}=3\)
=>-1,5m=3
=>m=-2
b: \(\lim\limits_{x\rightarrow-m}\dfrac{2x-3}{x+m}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow-m}2x-3=-2m-3\\\lim\limits_{x\rightarrow-m}x+m=0\end{matrix}\right.\)
=>x=-m là tiệm cận đứng duy nhất của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\)
Để x=-2 là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{2x-3}{x+m}\) thì -m=-2
=>m=2
c: \(\lim\limits_{x\rightarrow\dfrac{2}{b}}\dfrac{ax+1}{bx-2}=\infty\) vì \(\left\{{}\begin{matrix}\lim\limits_{x\rightarrow\dfrac{2}{b}}ax+1=a\cdot\dfrac{2}{b}+1\\\lim\limits_{x\rightarrow\dfrac{2}{b}}bx-2=b\cdot\dfrac{2}{b}-2=0\end{matrix}\right.\)
=>Đường thẳng \(x=\dfrac{2}{b}\) là tiệm cận đứng của đồ thị hàm số \(y=\dfrac{ax+1}{bx-2}\)
=>2/b=2
=>b=1
=>\(y=\dfrac{ax+1}{x-2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow+\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{ax+1}{x-2}=\lim\limits_{x\rightarrow-\infty}\dfrac{a+\dfrac{1}{x}}{1-\dfrac{2}{x}}=a\)
=>Đường thẳng y=a là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{ax+1}{x-2}\)
=>a=3
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\lim\limits_{x\rightarrow-\infty}\dfrac{1+\dfrac{1}{x}}{-\left(m^2+1\right)\sqrt[]{1-\dfrac{4}{x^2}}}=-\dfrac{1}{m^2+1}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{1}{m^2+1}\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận ngang
\(\lim\limits_{x\rightarrow2^+}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{3}{0}=\infty\)
\(\lim\limits_{x\rightarrow-2^-}\dfrac{x+1}{\left(m^2+1\right)\sqrt{x^2-4}}=\dfrac{-1}{0}=\infty\)
\(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy ĐTHS có 4 tiệm cận
tại sao nơi chỗ lim\(_{x->2^+}\) và limx->-2- ở dưới mẫu lại bằng 0 vậy ạ?
Ta có 
đồ thị hàm số luôn có TCN y = 1
Do đó để ycbt thỏa mãn 
Chọn C.
\(\lim\limits_{x\rightarrow+\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\lim\limits_{x\rightarrow+\infty}\dfrac{2019}{\sqrt{17-\dfrac{1}{x^2}}-m}=\dfrac{2019}{\sqrt{17}-m}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{2019x}{\sqrt{17x^2-1}-m\left|x\right|}=\dfrac{2019}{m-\sqrt{17}}\)
Với \(m\ne\sqrt{17}\Rightarrow\) đồ thị hàm số luôn có 2 tiệm cận ngang
Với \(m=\sqrt{17}\) đồ thị hàm số ko có tiệm cận ngang
Xét phương trình: \(\sqrt{17x^2-1}=m\left|x\right|\)
- Với \(m< 0\Rightarrow\) pt vô nghiệm \(\Rightarrow\) ko có tiệm cận đứng \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
- Với \(m\ge0\)
\(\Leftrightarrow17x^2-1=m^2x^2\Leftrightarrow\left(17-m^2\right)x^2=1\)
+ Nếu \(\left[{}\begin{matrix}m\ge\sqrt{17}\\m\le-\sqrt{17}\end{matrix}\right.\) pt vô nghiệm \(\Rightarrow\) ĐTHS có tối đa 2 tiệm cận (ktm)
+ Nếu \(-\sqrt{17}< m< \sqrt{17}\) pt có 2 nghiệm \(\Rightarrow\) ĐTHS có 2 tiệm cận đứng
Vậy \(m=\left\{0;1;2;3;4\right\}\) có 5 phần tử
Với \(m=0\) ko thỏa mãn
Với \(m\ne0\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=-\dfrac{1}{\sqrt{m}}\); \(\lim\limits_{x\rightarrow+\infty}\dfrac{x+1}{\sqrt{mx^2+1}}=\dfrac{1}{\sqrt{m}}\)
\(\Rightarrow\) Hàm có 2 TCN khi \(\sqrt{m}\) xác định \(\Rightarrow m>0\)
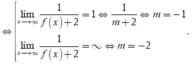
a: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(m-5\right)-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(m-5\right)x-1}{2x+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{m-5-\dfrac{1}{x}}{2+\dfrac{1}{x}}=\dfrac{m-5}{2}\)
=>Đường thẳng \(y=\dfrac{m-5}{2}\) là tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(m-5\right)x-1}{2x+1}\)
Để đường tiệm cận ngang \(y=\dfrac{m-5}{2}\) đi qua M(-2;1) thì \(\dfrac{m-5}{2}=1\)
=>m-5=2
=>m=7
b: \(\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
\(=\lim\limits_{x\rightarrow-\infty}\dfrac{\left(2m-1\right)+\dfrac{1}{x}-\dfrac{1}{x^2}}{1+\dfrac{1}{x^2}}=2m-1\)
=>\(y=2m-1\) là đường tiệm cận ngang của đồ thị hàm số \(y=\dfrac{\left(2m-1\right)x^2+x-1}{x^2+1}\)
=>2m-1=1
=>2m=2
=>m=1