1)Cho hàm số y = ax
-Hãy xác định hệ số a biết đồ thị của hàm số đã cho đi qua điểm A (-2;1) -Vẽ đồ thị của hàm số đã cho với a vừa tìm được 2) Hàm số y = f(x) được cho bởi công thức f(x) = 3x² + 5. Chứng minh rằng bới mọi giá trị của x thì hàm số đã cho luôn nhận giá trị dương.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2017
thay \(A\left(-2;1\right)\) và hàm số ta có : \(1=a.\left(-2\right)\Leftrightarrow1=-2a\Leftrightarrow a=\dfrac{-1}{2}\)
vậy \(a=\dfrac{-1}{2}\)
bài này mk nghỉ phải vẽ đường thẳng (d) mới đúng chứ
YK
2
CM
23 tháng 6 2017
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
a) Đồ thị của hàm số đi qua điểm A(2; 6) nên:
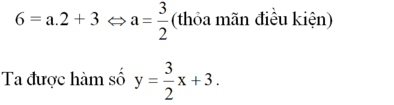
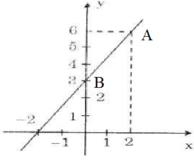
b) Vẽ đồ thị:
- Cho x = 0 thì y = 3 ta được B(0; 3).
Nối A, B ta được đồ thị hàm số
LV
1
DH
29 tháng 11 2021
dễ mà tự giải đi bạn ưi tui ko bít cách giải đâu nên đừn hỏi
CM
13 tháng 7 2017
Hàm số y = ax + 3 là hàm số bậc nhất nên a ≠ 0
Đồ thị của hàm số đi qua điểm A(2; 6) nên:
T
23 tháng 11 2018
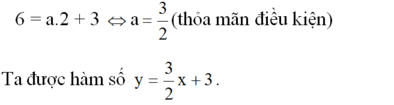
Vẽ đồ thị giùm nha! Giúp câu chứng minh thôi. Ở đây vẽ đồ thị xấu lém =,=
Ta có: \(y=f\left(x\right)=3x^2+5\)
Ta có: \(x^2\ge0\forall x\) (luôn đúng)
Nên \(3x^2\ge0\). do đó \(y=f\left(x\right)=3x^2+5\ge5\forall x\)
Vậy hàm số \(y=f\left(x\right)=3x^2+5\) luôn dương với mọi x. (đpcm)
Bài 2:
\(3x^2+5\ge5>0\forall x\)
nên f(x)>0 với mọi x