Question

[Nguyễn Thị Hương Giang]

Câu 59. Trong mặt phẳng tọa độ Oxy, cho đường thẳng A:3x - 4y -31 = 0 và điểm A(1;-7). Tìm tọa độ tâm của các đường tròn tiếp xúc với A tại A và có bán kính R = 5. 

A. 11(-2; –3), 12(4;–11). 

B. 11(2;3), 12(-4;11).

C. 11(2;–3), 12(4;–11). 

D. 11(-2;3), 12(4; -11).

Answer 1

[Nguyễn Linh Chi]

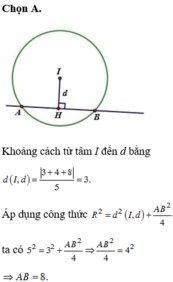
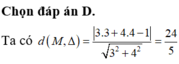
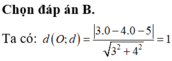
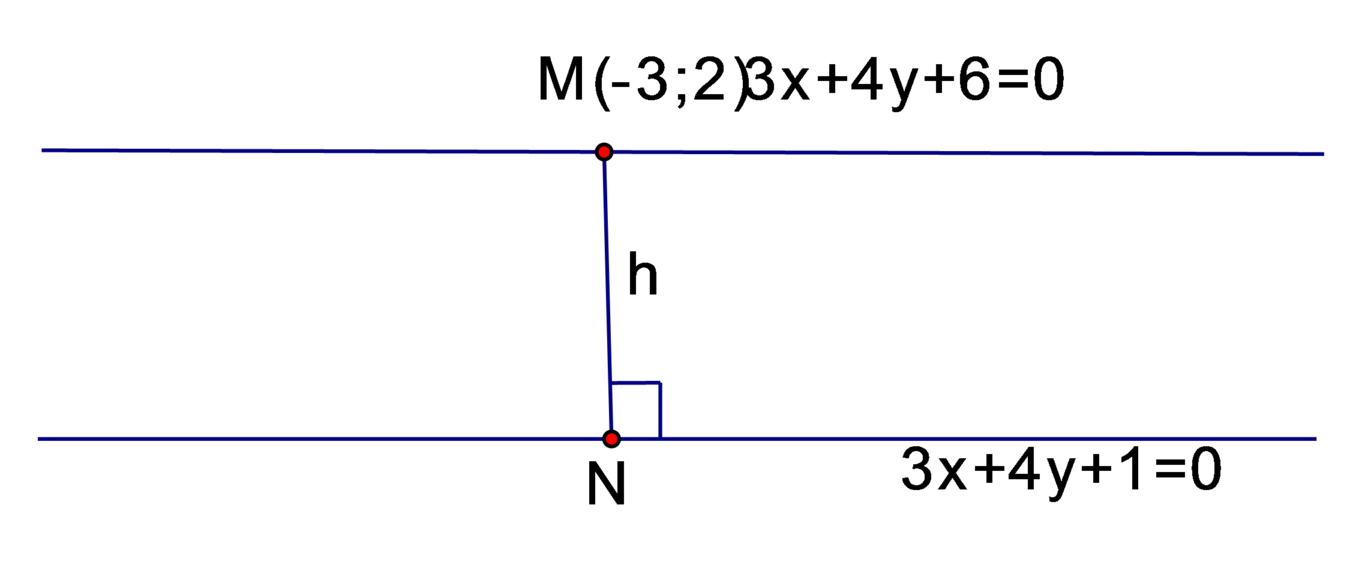
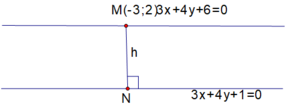
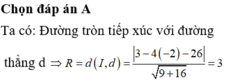
Đường thẳng a: 3x - 4y - 31 = 0 

Gọi I ( x; y ) là tâm của đương tròn cần tìm 

Ta có: d( I; a ) =  IA = 5 =>\(\frac{\left|3x-4y-31\right|}{\sqrt{3^2+4^2}}=5\) <=> \(\left|3x-4y-31\right|=25\)<=> 3x - 4y - 31 = 25 ( 1) hoặc 3x - 4y - 31 = -25 ( 2)

a có VTPT \(\overrightarrow{n}\) = ( 3; -4) => a có VTCP \(\overrightarrow{u}\) = ( 4; 3 )

Lại có: IA vuông góc với a   => ( 1- x ) . 4  + 3 ( - 7 - y ) = 0  <=> - 4x -3 y = 17 (3)

Từ (1) ; (3) =>  \(I_1\left(4;-11\right)\)

Từ (2) ; (3) =>  \(I_2\left(-2;-3\right)\)

Đáp án A