Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng (P) chứa điểm M(1;3;-2), cắt các tia Ox, Oy, Oz lần lượt tại các điểm A, B, C sao cho O A 1 = O B 2 = O C 4
A. x+2y+4z+1=0
B. 4x+2y+z-8=0
C. 2x-y-z-1=0
D. 4x+2y+z+1=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Ta có O M → = ( 3 ; - 4 ; 7 )
Vecto chỉ phương của trục Oz là k → = ( 0 ; 0 ; 1 )
Mặt phẳng (P) đi qua điểm M(3;-4;7) có vecto pháp tuyến
![]()
Vậy phương trình mặt phẳng
![]()

Đáp án A
Gọi N(0;1;0) là điểm thuộc trục Oy ⇒ M N → = ( - 1 ; 0 ; 1 )
Gọi ⇒ u → = ( 0 ; 1 ; 0 ) là một véc tơ chỉ phương của đường thẳng Oy.
![]()
là một véc tơ pháp tuyến của (P)
Suy ra phương trình mp(P) là
![]()

Ta có: O M ⇀ ( 1 ; 1 ; - 1 ) ; j ⇀ ( 0 ; 1 ; 0 )
Mặt phẳng (P) chứa trục Oy và đi qua điểm M(1;1-1) có một VTPT là n ⇀ = O M ⇀ ; j ⇀ = 1 ; 0 ; 1
Phương trình (P) là: 1 ( x - 0 ) + 0 + 1 ( z - 0 ) = 0 ⇔ x + z = 0
Chọn đáp án D.

Đáp án C
Phương pháp
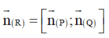
Cách giải: Ta có:
![]()
![]()
là 1 VTPT của mặt phẳng (R).
Vậy phương trình mặt phẳng (R):
![]()

Chọn D
Phương trình mặt chắn cắt tia Ox tại A (a; 0; 0), cắt tia Oy tại B (0; b; 0), cắt tia Oz C (0; 0; c) tại có dạng là ![]() (với a > 0, b > 0, c > 0).
(với a > 0, b > 0, c > 0).
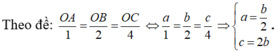
Vì M (1; 3; -2) nằm trên mặt phẳng (P) nên ta có:
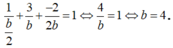
Khi đó a = 2, c = 8.
Vậy phương trình mặt phẳng (P) là:
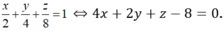
Đáp án B
Phương pháp
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a,b,c>0) =>OA =a, OB =b, OC=c
Viết phương trình mặt phẳng (P)
Cách giải :
Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a,b,c>0) =>OA =a, OB =b, OC=c
Khi đó phương trình mặt phẳng (P) là
Vậy phương trình mặt phẳng (P) là