hình bình hành có tọa độ đỉnh (4;-1) biết pt các đt chứa 2 cạnh là x-3y=0 và 2x+5y+6=0 . tìm tọa độ 3 đỉnh còn lại của hình bình hành đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1, Gọi tọa độ điểm D(x;y)
Ta có:\(\overrightarrow{AB}\left(8;1\right)\)
\(\overrightarrow{DC}\left(1-x;5-y\right)\)
Tứ giác ABCD là hình bình hành khi
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Leftrightarrow1-x=8;5-y=1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-7\\y=4\end{matrix}\right.\)
Vậy tọa độ điểm D(-7;4)

Từ giả thiết suy ra khoảng cách giữa 2 đường thẳng song song AB, CD bằng 4.
Từ đó, do A, B thuộc Ox nên C(c;4), D(d;4)
Vì 2 đường chéo AC, BD cắt nhau tại I nằm trên đường thẳng y=x nên ta có hệ :
\(\begin{cases}2x=c+1=d+2\\2x=0+4\end{cases}\)
Từ đó tìm được x=2, c=3, d=2.
Vậy C(3;4), D(2;4)
cho mình hỏi hình bình hành có diện tích bằng 4 thì sao suy ra được khoảng cách giữa 2 đường thẳng song song =4

Đáp án A
Gọi 3 đỉnh theo thứ tự là A, B,C
A B → = 1 ; 2 ; 3 , A C → = 6 ; 6 ; 4 S h b h = 2 S A B C = A B . A B . sin A = 2 83

Thay \(\left(-2;2\right)\) vào 2 pt 2 cạnh đều ko thỏa \(\Rightarrow\) 2 cạnh còn lại đi qua (-2;2)
2 cạnh đã cho ban đầu có vtpt lần lượt là (1;-1) và (1;3), do đó 2 cạnh còn lại cũng lần lượt nhận (1;-1) cà (1;3) là vtpt (do các cặp cạnh đối của hình bình hành song song)
Phương trình 2 cạnh còn lại là:
\(1\left(x+2\right)-1\left(y-2\right)=0\Leftrightarrow x-y+4=0\)
\(1\left(x+2\right)+3\left(y-2\right)=0\Leftrightarrow x+3y-4=0\)

\(a,\Rightarrow C,A,D\) \(thẳng\) \(hàng\Rightarrow\overrightarrow{CA}+\overrightarrow{CD}=\overrightarrow{0}\Leftrightarrow\overrightarrow{CA}=\overrightarrow{DC}\)
\(D\left(x;y\right)\Rightarrow\overrightarrow{CA}=\overrightarrow{DC}\Leftrightarrow\left\{{}\begin{matrix}-1-x=2\\-2-y=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=-2\end{matrix}\right.\)\(\Rightarrow D\left(-3;-2\right)\)
\(b,E\left(xo;yo\right)\Rightarrow\overrightarrow{AE}=\overrightarrow{BC}\)\(\Leftrightarrow\left\{{}\begin{matrix}xo-1=-3\\yo+2=-5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}xo=-2\\yo=-7\end{matrix}\right.\)\(\Rightarrow E\left(-2;-7\right)\)
\(c,\Rightarrow G\left(xG;yG\right)\Rightarrow\left\{{}\begin{matrix}xG=\dfrac{1+2-1}{3}=\dfrac{2}{3}\\yG=\dfrac{-2+3-2}{3}=-\dfrac{1}{3}\end{matrix}\right.\)\(\Rightarrow G\left(\dfrac{2}{3};-\dfrac{1}{3}\right)\)

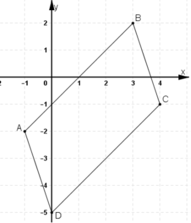
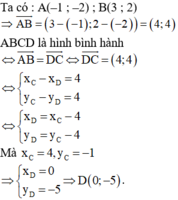
Gọi hình bình hành ABCD có A(4; -1)
Nhận thấy: A∉ (d1) x - 3y = 0; A∉ (d2); 2x + 5y + 6 =0
=> d1; d2 là BC và DC
Giả sử: BC: x -3y =0 ; CD: 2x + 5y +6 =0
=> Tọa độ đỉnh C là nghiệm của hệ: \(\left\{{}\begin{matrix}x-3y=0\\2x+5y+6=0\end{matrix}\right.\)
=> C(\(\frac{-18}{11};\frac{-6}{11})\)
Phương trình AD: x + 3y -1 = 0
=> Tọa độ đỉnh D là nghiệm của hệ: \(\left\{{}\begin{matrix}x+3y-1=0\\2x+5y+6=0\end{matrix}\right.\)
=> D(-23 ; 8)
Phương trình AB: 2x + 5y - 3 = 0
=> Tọa độ đỉnh B là nghiệm của hệ: \(\left\{{}\begin{matrix}2x+5y-3=0\\x-3y=0\end{matrix}\right.\)
=> B(\(\frac{9}{11};\frac{3}{11})\)