Cho ba số x ; y ; z khác 0 và \(\frac{1}{x}\)+ \(\frac{1}{y}+\frac{1}{z}=0\). Tính giá trị của biểu thức sau
P = \(\frac{2017xyz}{3}\cdot\left(\frac{1}{^{x^3}}+\frac{1}{y^3}+\frac{1}{z^3}\right)\)
giải hộ nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Theo giả thiết ta có: x + 2 y = 10 2 x y = 16 ⇒ y = 8 x x + 16 x = 10 ⇒ 2 y = 16 x x 2 - 10 x + 16 = 0 ⇔ [ x = 8 x = 2 2 y = 16 x
⇒ [ x = 8 2 y = 2 x = 2 2 y = 8 ⇒ x - 2 y = 6 .

Chọn C.
Theo tính chất của cấp số cộng và cấp số nhân ta có
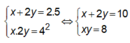
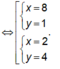
Vậy |x-2y| = 6


\(-\) Do \(c^x\) nghịch biến\(,a^x,b^x\) đồng biến\(\Rightarrow c< 1,a>1,b>1\Rightarrow c\) nhỏ nhất \(\Rightarrow\)Loại \(C,D\)
\(-\) Dựa vào đồ thị ta thấy\(,b^x\) có đồ thị đi lên cao hơn so với \(a^x\Rightarrow b>a\Rightarrow\) Chọn \(A\)
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\)
\(=>\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)^3=0\)
\(=>\left(\frac{1}{x}+\frac{1}{y}\right)^3+\frac{1}{z^3}+3\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right).\left(\frac{1}{x}+\frac{1}{y}\right)\frac{1}{z}=0\)
\(=>\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}+3\left(\frac{1}{x}+\frac{1}{y}\right)\frac{1}{xy}+3.0.\frac{1}{z}=0\)(do\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\))
\(=>\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}+3.\left(\frac{1}{x}+\frac{1}{y}\right)\frac{1}{xy}=0\)\(\left(1\right)\)
Mà \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0=>\frac{1}{x}+\frac{1}{y}=-\frac{1}{z}\)\(\left(2\right)\)
Từ (1) và (2) => \(\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}-3\frac{1}{xyz}=0\)
\(=>\frac{1}{x^3}+\frac{1}{y^3}+\frac{1}{z^3}=3\frac{1}{xyz}\)
Thay vào P ta có:
\(P=\frac{2013xyz}{3}.3.\frac{1}{xyz}=2017\)