Cho ba đường thẳng sau:
y = 2/5x + 1/2 (d1) ;
y = 3/5x - 5/2 (d2) ;
y = kx + 3,5 (d3)
Hãy tìm giá trị của k để sao cho ba đường thẳng đồng quy tại một điểm.
Help me! Thanks so much!!!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

* Trước hết tìm giao điểm của hai đường thẳng ( d 1 ) và ( d 2 ).
- Tìm hoành độ của giao điểm:
2/5x + 1/2 = 3/5x - 5/2 ⇔ 1/5x = 6/2 ⇔ x = 15.
- Tìm tung độ giao điểm:
y = 2/5.15 + 1/2 = 6,5.
*Tìm k (bằng cách thay tọa độ của giao điểm vào phương trình ( d 3 ).
6,5 = k.15 + 3,5 ⇔ 15k = 3 ⇔ k = 0,2.
Trả lời: Khi k = 0,2 thì ba đường thẳng đồng quy tại điểm (15; 6,5).

Tọa độ giao điểm của ( d 1 ) và ( d 2 ) là nghiệm của hệ phương trình:
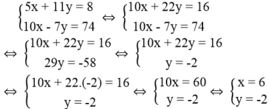
Tọa độ giao điểm của ( d 1 ) và ( d 2 ) là (x; y) = (6; -2)
Để ba đường thẳng ( d 1 ), ( d 2 ), ( d 3 ) đồng quy thì ( d 3 ) phải đi qua giao điểm của ( d 1 ) và ( d 2 ), nghĩa là (x; y) = (6; -2) nghiệm đúng phương trình đường thẳng ( d 3 ).
Khi đó ta có: 4m.6 + (2m – 1).(-2) = m + 2
⇔ 24m – 4m + 2 = m + 2 ⇔ 19m = 0 ⇔ m = 0
Vậy với m = 0 thì 3 đường thẳng ( d 1 ), ( d 2 ), ( d 3 ) đồng quy.

Do các đường thẳng đôi một cắt nhau tại các điểm A, B, C nên các điểm cách đều các cạnh gồm tâm đường tròn nội tiếp và ba tâm đường tròn bàng tiếp.
Vậy có tất cả 4 điểm M cách đều ba đường thẳng đã cho.
đáp án D

+) Thay tọa độ điểm M (0; 5) vào phương trình đường thẳng d2 ta được 5 = 5 . 0 – 1 ⇔ 5 = − 1 (vô lý)
+) Xét tính đồng quy của ba đường thẳng
* Phương trình hoành độ giao điểm của d 1 v à d 2 :
− x + 5 = 5 x – 1 ⇔ 6 x = 6 ⇔ x = 1 ⇒ y = − 1 + 5 ⇒ y = 4
Suy ra tọa độ giao điểm của d 1 v à d 2 là (1; 4)
* Thay x = 1 ; y = 4 vào phương trình đường thẳng d3 ta được 4 = − 2 . 1 + 6 4 = 4 (luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm N (1; 4)
Đáp án cần chọn là: B

`(d1) //// (d2) <=> {(a = a'),(b \ne b'):}`
`<=>{(m^2 + 1 = 5),(1 \ne 2\text{ (Luôn đúng)}):}`
`<=> m^2 = 4`
`<=>m = +-2`
Vậy `m = +-2` thì `(d1) //// (d2)`

a,Giao của d1 và d2 là điểm có hoành độ thỏa mãn pt :
x -1 = - x + 3
x - 1 + x - 3 = 0
2x - 4 = 0
2x = 4
x = 2
thay x = 2 vào pt y = x - 1 => y = 2 - 1 = 1
Giao của d1 và d2 là A ( 2; 1)
b, để d1; d2; d3 đồng quy thì d3 phải đi qua giao điểm của d1 và d2 là điểm A ( 2; 1)
Thay tọa độ điểm A vào pt d3 ta có :
2.(m-2) .2 + (m-1) = 1
4m - 8 + m - 1 = 1
5m - 9 = 1
5m = 10
m = 2
vậy với m = 2 pt d3 là y = 2 -1 = 1 thì d1; d2 ; d3 đồng quy tại 1 điểm
c, vẽ đồ thị hàm số câu này dễ bạn tự làm nhé
Giao d1 với Ox là điểm có tung độ y = 0 => x -1 = 0 => x = 1
Vậy giao d1 với Ox là điểm B( 1;0)
độ dài OB là 1
Giao d1 với trục Oy điểm có hoành độ x = 0 => y = 0 - 1 = -1
Vậy giao d1 với Oy là điểm C ( 0; -1)
Độ dài OC = |-1| = 1
vẽ đồ thị bạn tự vẽ nhé
d, Xét tam giác vuông OBC có
OB = OC = 1 ( cmt)
=> tam giác OBC vuông cân tại O
=> góc OBC = ( 1800 - 900): 2 = 450
Kết luận d1 tạo với trục Ox một góc bằng 450

Xét phương trình hoành độ giao điểm của d 1 v à d 3 :
6 − 5 x = 3 x + 2 ⇔ 8 x = 4 ⇔ x = 1 2 ⇒ y = 7 2 . Suy ra giao điểm của d 1 v à d 3 là M 1 2 ; 7 2
Để ba đường thẳng trên đồng quy thì M d2 nên 7 2 = ( m + 2 ) . 1 2 + m
⇔ 3 m 2 + 1 = 7 2 ⇔ m = 5 3
Vậy m = 5 3
Đáp án cần chọn là: A

Đáp án C
Hoành độ giao điểm của d 1 và d 2 là nghiệm phương trình:
2x + 1 = x -1 nên x = -2
Với x = -2 thì y = 2. (-2) + 1 = -3
Vậy 2 đường thẳng d 1 và d2 cắt nhau tại A(-2; -3).
Để ba đường thẳng đã cho đồng quy thì điểm A(-2; -3) thuộc đồ thị hàm số y = (m + 1)x – 2
Suy ra: -3 = (m + 1).(-2) - 2
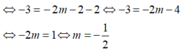

Ba đường thẳng đã cho đồng quy khi hệ 2 x + 3 y = 1 x - y = 2 m x + ( 2 m + 1 ) y = 2 có nghiệm duy nhất.
Xét hệ gồm hai phương trình (1) và (2) :
2 x + 3 y = 1 ( 1 ) x - y = 2 ( 2 ) ⇔ 2 x + 3 y = 1 2 x - 2 y = 4 ⇔ 2 x + 3 y = 1 5 y = - 3 ⇔ x = 7 5 y = - 3 5
Hệ này có nghiệm duy nhất là 7 5 ; - 3 5 .
Để ba đường thẳng đã cho đồng quy thì 7 5 ; - 3 5 cũng là nghiệm của phương trình (3), tức là
m . 7 5 + 2 m + 1 . - 3 5 = 2 ⇔ 7 m - 3 2 m + 1 = 10 ⇔ 7 m - 6 m - 3 = 10 ⇔ m = 13 .

a) Phương trình hoành độ giao điểm của d₁ và d₂
x + 2 = 5 - 2x
⇔ x + 2x = 5 - 2
⇔ 3x = 3
⇔ x = 1
Thay x = 1 vào d₁ ta có:
y = 1 + 2 = 3
⇒ Giao điểm của d₁ và d₂ là A(1; 3)
Thay tọa độ điểm A vào d₃ ta có:
VT = 3
VP = 3.1 = 3
⇒ VT = VP
Hay A ∈ d₃
Vậy d₁, d₂ và d₃ đồng quy
b) Thay tọa độ điểm A(1; 3) vào d₄ ta có:
m.1 + m - 5 = 3
⇔ 2m - 5 = 3
⇔ 2m = 3 + 5
⇔ 2m = 8
⇔ m = 8 : 2
⇔ m = 4
Vậy m = 4 thì d₁, d₂ và d₄ đồng quy
Xét PTHĐGĐ của (d1) và (d2)
\(\frac{2}{5}x+\frac{1}{2}=\frac{3}{5}x-\frac{5}{2}\)
\(\Leftrightarrow x=15\)\(\Rightarrow y=\frac{13}{2}\)\(\Rightarrow\left(15;\frac{13}{2}\right)\)
Để 3 đt đồng quy\(\Leftrightarrow\left(15;\frac{13}{2}\right)\in\left(d_3\right)\)
Thay x=15; y=\(\frac{13}{2}\) vào (d3) có:
\(15k+3,5=\frac{13}{2}\Leftrightarrow k=\frac{1}{5}\)