Cho phương trình bậc hai: x 2 – 5x – 2 = 0. Không giải phương trình để tìm 2 nghiệmx1 ; x2 . Hãy tính giá trị của biểu thức: A =\(\dfrac{x1-1}{x2-1}+\dfrac{x2-1}{x1-1}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi x1,x2 là các nghiệm của phương trình đã cho
Áp dụng hệ thức Vi-et,ta có :
x1 + x2 = -5 ; x1x2 = -1
gọi y1,y2 là các nghiệm của phương trình phải lập,ta được :
y1 + y2 = x14 + x24 , y1y2 = x14x24
Ta có : x12 + x22 = ( x1 + x2 )2 - 2x1x2 = 25 + 2 - 27
Do đó : y1 + y2 = x14 + x24 = ( x12 + x22 )2 - 2x12x22 = 729 - 2 = 727
y1y2 = ( x1x2 )4 = 1
Từ đó pt phải lập có dạng : y2 - 727y + 1 = 0
Ta co: P = -1 <0
=> (1) có 2 nghiệm phân biệt khác dấu
Gọi hai nghiệm đó là \(x_1;x_2\)
=> \(x_1+x_2=-5;x_1.x_2=-1\)
Ta có: \(\left(x_1.x_2\right)^4=\left(-1\right)^4=1\)
\(\left(x_1\right)^4+\left(x_2\right)^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2\)
\(=\left[\left(-5\right)^2-2.\left(-1\right)\right]^2-2.\left(-1\right)^2\)
\(=727\)
=> Phương trình có các nghiệm lũy thừa bậc 4 của các nghiệm phương trình (1) là:
\(x^2-727x+1=0\)

Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1

Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
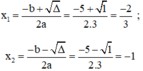
Vậy phương trình có hai nghiệm là -1 và 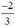

a) Bình phương hai vế của phương trình\(\sqrt {{x^2} - 3x + 2} = \sqrt { - {x^2} - 2x + 2} \)ta được:
\({x^2} - 3x + 2 = - {x^2} - 2x + 2\)(1)
Giải phương trình trên ta có:
\((1) \Leftrightarrow 2{x^2} - x = 0\)
\( \Leftrightarrow x(2x - 1) = 0\)
\( \Leftrightarrow x = 0\) hoặc \(x = \frac{1}{2}\)
b) Thử lại ta có:
Với x=0, thay vào phương trình đã cho ta được: \(\sqrt {{0^2} - 3.0 + 2} = \sqrt { - {0^2} - 2.0 + 2} \Leftrightarrow \sqrt 2 = \sqrt 2 \) (luôn đúng)
Với \(x = \frac{1}{2}\), thay vào phương trình đã cho ta được:
\(\sqrt {{{\left( {\frac{1}{2}} \right)}^2} - 3.\frac{1}{2} + 2} = \sqrt { - {{\left( {\frac{1}{2}} \right)}^2} - 2.\frac{1}{2} + 2} \Leftrightarrow \sqrt {\frac{3}{4}} = \sqrt {\frac{3}{4}} \) (luôn đúng)
Vậy các giá trị x tìm được ở câu a thỏa mãn phương trình đã cho.