Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mp qua M và song song với mp(SIC); biết AM=x. Thiết diện tạo bởi mp(P) và tứ diện SABC có chu vi là: A. 3x(1+
3
) B. 2x(1+
3
) C. x(1+
3
) D. Không tính...
Đọc tiếp
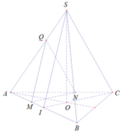
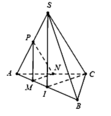
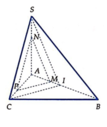
Cho tứ diện đều SABC. Gọi I là trung điểm của AB, M là một điểm di động trên đoạn AI. Gọi (P) là mp qua M và song song với mp(SIC); biết AM=x. Thiết diện tạo bởi mp(P) và tứ diện SABC có chu vi là:
A. 3x(1+ 3 )
B. 2x(1+ 3 )
C. x(1+ 3 )
D. Không tính được
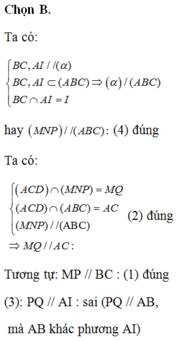
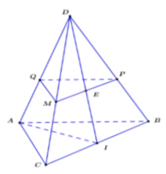
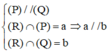
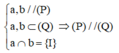
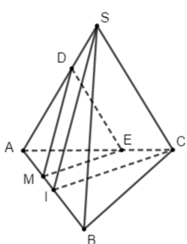
Đáp án B
Trong (ABC), kẻ đường thẳng d đi qua M song song CI
d cắt AC tại H
Trong (SAB) kẻ đường thẳng x đi qua M và song song SI
X cắt SA tại J
⇒ (MHJ) là thiết diện cần tìm
Gọi tứ diện đều cạnh 2a ⇒ AI = a
Ta có AM = x và M J S I = A M A I (MJ // SI theo cách dựng)
A M A I = M H C I (MH // CI theo cách dựng)
J H S C = A H A C = A M A I
⇒ MJ = x a . 3 a = x 3
MH = x a . 3 a = x 3
JH = x a . 2 a = 2x
Chu vi thiết diện MHJ là: x 3 + x 3 + 2x = 2x ( 3 + 1 )