Cho tam giác ABC cân tại A, H là trung điểm BC, kẻ HE vuông góc AC tại E; HF vuông góc AB tại F
1. CMR tam giác ABH = tam giác ACH
2. CMR tam giác AEF cân
3. CMR EF song song BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 3 2023
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `BAH` và Tam giác `CAH` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`HB = HC ( H` là trung điểm của `BC)`
`=> \text {Tam giác BAH = Tam giác CAH (c-g-c)}`
`->`\(\widehat{BAH}=\widehat{CAH} (\text {2 góc tương ứng})\)
`b,` Xét Tam giác `HEA` và Tam giác `BDA` có:
`AH` chung
\(\widehat{EAH}=\widehat{DAH} (a)\)
\(\widehat{HEA}=\widehat{HDA}=90^0\)
`=> \text {Tam giác HEA = Tam giác BDA (ch-gn)}`
`-> HE = HD (\text {2 cạnh tương ứng})`
`\text {Xét Tam giác HDE: HD = HE} -> \text {Tam giác HDE cân tại H}`
12 tháng 1 2024
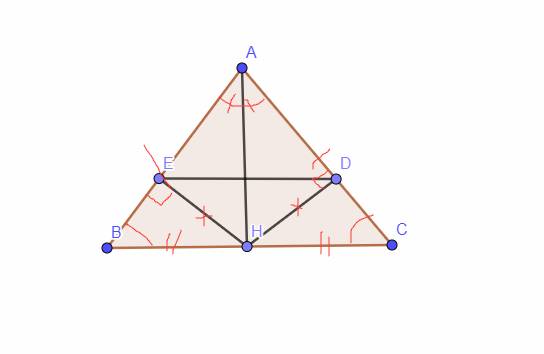
1: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
=>HB=HC
=>H là trung điểm của BC
2: Ta có: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
ΔAHB vuông tại H
=>\(HA^2+HB^2=AB^2\)
=>\(HA^2=10^2-6^2=64\)
=>\(HA=\sqrt{64}=8\left(cm\right)\)
3: Xét ΔAHN có
AF là đường cao
AF là đường trung tuyến
Do đó: ΔAHN cân tại A
=>AH=AH
4: Xét ΔAHM có
AE là đường trung tuyến
AE là đường cao
Do đó: ΔAHM cân tại A
=>AM=AH
Ta có: ΔAHN cân tại A
mà AC là đường cao
nên AC là phân giác của góc HAN
=>\(\widehat{HAN}=2\cdot\widehat{HAC}\)
Ta có: ΔAHM cân tại A
mà AB là đường cao
nên AB là phân giác của góc HAM
=>\(\widehat{HAM}=2\cdot\widehat{HAB}\)
Ta có: AM=AH
AH=AN
Do đó: AM=AN
Ta có: \(\widehat{HAM}+\widehat{HAN}=\widehat{MAN}\)
=>\(\widehat{MAN}=2\cdot\left(\widehat{HAB}+\widehat{HAC}\right)\)
=>\(\widehat{MAN}=2\cdot\widehat{BAC}\)
Để A là trung điểm của MN thì AM=AN và góc MAN=180 độ
=>góc MAN=180 độ
=>\(2\cdot\widehat{BAC}=180^0\)
=>\(\widehat{BAC}=90^0\)
29 tháng 8 2023
a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
BA=BH
Do đó; ΔBAE=ΔBHE
b: ΔBAE=ΔBHE
=>EA=EH
=>ΔEAH cân tại E
c: BA=BH
EA=EH
=>BE là trung trực của AH
d: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại E
Do đó: E là trực tâm
=>BE vuông góc KC
7 tháng 4 2022
a: Xét ΔHDB vuông tại D và ΔHEC vuông tại E có
HB=HC
\(\widehat{B}=\widehat{C}\)
Do đó: ΔHDB=ΔHEC
b: Ta có: ΔHDB=ΔHEC
nên BD=EC
Ta có: AD+DB=AB
AE+EC=AC
mà BD=CE
và AB=AC
nên AD=AE
6 tháng 4 2023
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: ΔABC cân tại A
mà AH là trung tuyến
nên AH là phân giác
c: Xet ΔAEH vuôngtại E và ΔAFH vuông tại F có
AH chung
góc EAH=góc FAH
=>ΔAEH=ΔAFH
=>AE=AF
=>ΔAEF cân tại A
mà AI là phân giác
nên AI là trung tuyến
a, xét tam giác ABH và tam giác ACH có AH chung
góc AHC = góc AHB = 90
AB = AC do tam giác ABC cân tại A (gt)
=> tam giác ABH = tam giác ACH (ch-cgv)
b, ta giác ABH = tam giác ACH (câu a)
=> HB = HC (đn)
xét tam giác BHF và tam giác CHE có : góc BFH = góc CEH = 90
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> tam giác BHF = tam giác CHE (ch-gn)
=> BF = CE (đn)
AB = AC (câu a)
BF + FA = AB
CE + AE = AC
=> FA = AE
=> tam giác AFE cân tại A (đn)
c, tam giác AFE cân tại A (Câu b)
=> góc AFE = (180 - góc BAC) : 2 (tc)
tam giác ABC cân tại A (gt) => góc ABC = (180 - góc BAC) : 2 (tc)
=> góc AFE = góc ABC mà 2 góc này đồng vị
=> FE // BC (định lí)