Cho tứ diện ABCD. Trên các cạnh AD và BC lần lượt lấy M, N sao cho AM = 3MD; BN = 3NC. Gọi P, Q lần lượt là trung điểm của AD và BC. Chứng minh các vectơ M N → , D C → , P Q → đồng phẳng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
23 tháng 8 2019
a) Ta có AD = BC; AD // BC (gt), AM = CN (gt)
⇒ AD – AM = BC – CN
Hay DM = BN
Lại có DM // BN
Do đó MNDN là hình bình hành ⇒ BM // DN
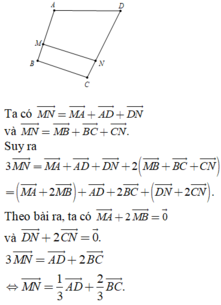


+) Do AM = 3MD; BN = 3NC suy ra:
+) Do P và Q lần lượt là trung điểm của AD và BC nên :
- Từ (1) và (2) suy ra: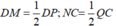
- Suy ra: M là trung điểm của DP; N là trung điểm CQ.
+) Ta có: