Cho tam giác ABC có AB=25cm; AC=26cm. Đường cao AH=24cm. Tính Bc trong 2 trường hợp góc B là góc nhọn và góc B là góc tù
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


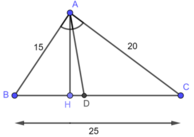
a) Trong tam giác ABC, ta có: AD là đường phân giác của:
⇒\(\dfrac{DB}{DC}\)=\(\dfrac{AB}{AC}\)
Mà AB = 15cm và AC = 20cm ( gt )
Nên \(\dfrac{DC}{DB}\)=\(\dfrac{15}{20}\)
⇒\(\dfrac{DB}{DB+DC}\)=\(\dfrac{15}{15+20}\)( Tính chất tỉ lệ thức đã học ở lớp 7 )
⇒\(\dfrac{DB}{BC}\)=\(\dfrac{15}{35}\)⇒DB=\(\dfrac{15}{35}\).BC=\(\dfrac{15}{35}\).25=\(\dfrac{75}{5}\)(cm)
b) Kẻ AH⊥BC
Ta có:\(S_{ABD}\)=\(\dfrac{1}{2}\)AH.BD
\(S_{ACD}\)=\(\dfrac{1}{2}\)AH.CD
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.CD}\)=\(\dfrac{BD}{DC}\)
Mà \(\dfrac{DB}{DC}\)=\(\dfrac{15}{12}\)=\(\dfrac{3}{4}\)
⇒\(\dfrac{S_{ABD}}{S_{ACD}}\)=\(\dfrac{3}{4}\)(đpcm)

Ta có tam giác ABC vuông tại A => BC2 = AB2 + AC2
=> AC2 = BC2 - AB2 = 252 - 202 = 625 - 400 = 225
=> AC = 15
Vì tam giác ABC vuông tại A => BC^2=AB^2+AC^2 ( theo định lí Pi-ta-go)
<=> AC^2=BC^2-AB^2
<=> AC^2=625-400
<=> AC^2=225
<=> AC=15

a) Xét tam giác ABC có:
BD là tia phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BD}{DC}=\dfrac{15}{20}=\dfrac{3}{4}\)(tính chất)
\(\Rightarrow\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{BC}{7}=\dfrac{25}{7}\)(tính chất dãy tỉ số bằng nhau)
\(\Rightarrow\left\{{}\begin{matrix}DB=\dfrac{25.3}{7}=\dfrac{75}{7}\left(cm\right)\\DC=\dfrac{25.4}{7}=\dfrac{100}{7}\left(cm\right)\end{matrix}\right.\)
b) Kẻ đường cao AH của tam giác ABC
\(\Rightarrow\dfrac{S_{ACD}}{S_{ABC}}=\dfrac{\dfrac{1}{2}.AH.DC}{\dfrac{1}{2}.AH.BC}=\dfrac{DC}{BC}=\dfrac{100}{7}:25=\dfrac{4}{7}\)
a: Xét ΔABC có
AD là đường phân giác ứng với cạnh BC
nên \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\)
hay \(\dfrac{BD}{15}=\dfrac{CD}{20}\)
mà BD+CD=25cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: \(BD=\dfrac{75}{7}cm;CD=\dfrac{100}{7}cm\)

A B C H 24 25 26
Tam giác AHB vuông tại H => Áp dụng định lý pitago ta có :
AB2 = AH2 + HB2 => HB2 = AB2 - AH2 = 252 - 242 = 625 - 576 = 49 = 72
=> HB = 7
Tam giác AHC vuông tại H => Áp dụng định lý pitago ta có :
AC2 = CH2 + AH2 => CH2 = AC2 - AH2 = 262 - 242 = 676 - 576 = 100 = 102
=> CH = 10
=> BC = HB + CH = 7 + 10 = 17 (cm)
Vậy BC = 17 (cm)
Giải:
A B H C 25 24 26
Áp dụng định lý Py-ta-go vào tam giác AHB (tam giác AHB vuông tại H)
=> AB2 = AH2 + HB2
=> HB2 = AB2 - AH2
=> HB2 = 252 - 242
=> HB = 625 - 526 = 49 = 72
=> HB = 7
Áp dụng định lý Py-ta-go và tam giác AHC (tam giác AHC vuông H)
=> AC2 = AH2 + HC2
=> HC2 = AC2 - AH2
=> HC2 = 262 - 242
=> HC = 676 - 576 = 100 = 102
=> HC = 10
=> BC = BH + HC
BC = 7 + 10 = 17 (cm)
Vậy BC = 17 cm.

\(BC=BH+CH=25+144=169\left(cm\right)\)
Áp dụng hệ thức lượng vào tam giác ABC vuông tại A có đường cao AH có:
\(AH^2=HB.HC=25.144\Rightarrow AH=\sqrt{3600}=60\left(cm\right)\)
\(AB^2=BH.BC=25.169=4225\Rightarrow AB=\sqrt{4225}=65\left(cm\right)\)
\(AC^2=CH.CB=144.169=24336\Rightarrow AC=\sqrt{24336}=156\left(cm\right)\)

A B C D E
a. ta có \(\hept{\begin{cases}\frac{DB}{DC}=\frac{AB}{AC}=\frac{10}{25}=\frac{2}{5}\\BD+DC=BC=30\end{cases}\Rightarrow\hept{\begin{cases}DB=\frac{60}{7}\\DC=\frac{150}{7}\end{cases}}}\)
mà \(\frac{DE}{AB}=\frac{CD}{CB}=\frac{5}{7}\Rightarrow DE=\frac{50}{7}cm\)
b.ta có \(\frac{S_{ABD}}{S_{ABC}}=\frac{BD}{BC}=\frac{2}{7}\Rightarrow S_{ABD}=\frac{120.2}{7}=\frac{240}{7}cm^2\Rightarrow S_{ACD}=S_{ABC}-S_{ABD}=\frac{600}{7}\)
mà
\(\frac{S_{AED}}{S_{ADC}}=\frac{AE}{AC}=\frac{BD}{BC}=\frac{2}{7}\Rightarrow S_{AED}=\frac{600}{7}\frac{.2}{7}=\frac{1200}{49}cm^2\Rightarrow S_{CDE}=S_{ACD}-S_{AED}=\frac{3000}{49}\)