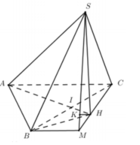
Cho tam giác ABC có góc A bằng 900; AC > AB. Kẻ AH vuông góc với BC. Trên BC lấy điểm D sao cho HD = HB. Kẻ CE vuông góc với AD kéo dài. Chứng minh:a) Tam giác BAD cân.b) CD là tia phân giác của góc ECA.c) Gọi giao điểm của AH và CE là K. Chứng minh: KD // AB.d) Tìm điều kiện của tam giác ABC để tam giác AKC đều.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
25 tháng 4 2017
Ta có: C ^ = P ^ mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần thêm điều kiện A C = M P
Đáp án A
YB
2

CM
8 tháng 4 2019
Ta có hai tam giác ABC và tam giác NPM có B C = P M , B ^ = P ^ = 90 0 mà BC, PM là hai cạnh góc vuông của tam giác ABC và NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông thì ta cần thêm điều kiện CA = MN
Đáp án C