Cho hai đường thẳng tt' và yy' cắt nhau tại A, tạo thành 4 góc A1 ;A2; A3; A4 . Tính các góc A3; A4 trong các trường hợp :
a) A1+A3 =100o
b)A1 -A2 = 100o
c)2A1 =A4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai đường thẳng xx' và yy' cắt nhau tại O : Đúng
b) Hai đường thẳng xx' và yy' tạo thành 4 góc vuông : Sai
c) Mỗi đường thẳng là đường phân giác của một góc bẹt : Đúng

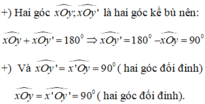
Do đó, mỗi đường thẳng là đường phân giác của một góc bẹt.
a. Đúng
b. Đúng
c. Đúng
O t t' y y' 1 2 3 4
Giải: a) Ta có: \(\widehat{A_1}=\widehat{A_3}\) (đối đỉnh)
mà \(\widehat{A_1}+\widehat{A_3}=100^0\)
=> \(2.\widehat{A_3}=100^0\)
=> \(\widehat{A_3}=100^0:2=50^0\)
Ta lại có: \(\widehat{A_3}+\widehat{A_4}=180^0\)(kề bù)
=> \(\widehat{A_4}=180^0-\widehat{A_3}=180^0-50^0=130^0\)
b) Ta có : \(\widehat{A_1}+\widehat{A_2}=180^0\) (kề bù)
Mà \(\widehat{A_1}-\widehat{A_2}=100^0\)
=> \(2.\widehat{A_1}=280^0\)
=> \(\widehat{A_1}=280^0:2=140^0\)
=> \(\widehat{A_2}=140^0-100^0=40^0\)
Ta lại có: +) \(\widehat{A_1}=\widehat{A_3}\)(đối đỉnh)
Mà \(\widehat{A_1}=140^0\) => \(\widehat{A_3}=140^0\)
+) \(\widehat{A_2}=\widehat{A_4}\) (đối đỉnh)
Mà \(\widehat{A_2}=40^0\) => \(\widehat{A_4}=40^0\)
c) Ta có: \(\widehat{A_1}+\widehat{A_4}=180^0\) (kề bù)
=> \(\widehat{A_1}+2.\widehat{A_1}=180^0\)
=> \(3.\widehat{A_1}=180^0\)
=> \(\widehat{A_1}=180^0:3=60^0\)
=> \(\widehat{A_4}=180^0-60^0=120^0\)
Ta lại có: \(\widehat{A_1}=\widehat{A_3}\) (đối đỉnh)
Mà \(\widehat{A_1}=60^0\) => \(\widehat{A_3}=60^0\)