3TÌM cặp đg thẳng là phân giác của các góc hợp bởi 2 đg thẳng denta 1; 3x +4y +1=0 và denta 2: x -2y +4=0
Mk cần câu ni gấp lắm.ạ bn nào.giúp mk vs
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 4 2020
1. Tìm cosin góc giữa 2 đg thẳng denta 1 : 10x +5y -1=0 và denta 2 : x = 2+t ; y = 1-t
\(\Delta\left(1\right):10x+5y-1=0\)
\(\Delta\left(2\right):\left\{{}\begin{matrix}x=2+t\\y=1-t\end{matrix}\right.\)
\(\Delta\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}t=x-2\\y=1-\left(x-2\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}t=x-2\\y=1-x+2\end{matrix}\right.\Leftrightarrow x+y-3=0\)
Ta có phương trình tổng quát của \(\Delta\left(2\right)\)là \(x+y-3=0\)
\(cos\left(\Delta\left(1\right),\Delta\left(2\right)\right)=\frac{\left|a_1.a_2+b_1.b_2\right|}{\sqrt{a_1^2+b_1^2}\sqrt{a_2^2+b_2^2}}\)
\(=\frac{\left|10+5\right|}{\sqrt{1+1}.\sqrt{100+25}}=\frac{15}{5\sqrt{10}}\)
Bấm SHIFT COS\(\left(\frac{15}{5\sqrt{10}}\right)\)=o'''
\(=18^o26'5,82''\)
bài 2,3,4 tương tự vậy.
AH
Akai Haruma
Giáo viên
20 tháng 4 2020
Lời giải:
PT đường phân giác đi qua điểm $O$ nên có dạng $y=kx$
Gọi $M$ là điểm nằm trên đường phân giác, có tọa độ $(a,b)$
Theo tính chất đường phân giác:
\(d(M,\Delta)=d(M,Ox)\)
\(\Leftrightarrow \frac{|a+b|}{\sqrt{1^2+1^2}}=\frac{|b|}{\sqrt{1^2+0^2}}\Leftrightarrow |a+b|=\sqrt{2}|b|\)
\(\Rightarrow \left[\begin{matrix} a+b=\sqrt{2}b\\ a+b=-\sqrt{2}b\end{matrix}\right.\Rightarrow \left[\begin{matrix} a=b(\sqrt{2}-1)\\ a=b(-\sqrt{2}-1)\end{matrix}\right.\Rightarrow \left[\begin{matrix} b=(1+\sqrt{2})a\\ b=(1-\sqrt{2})a\end{matrix}\right.\)
Do đó PT đường phân giác có dạng
$y=(1+\sqrt{2})x$ hoặc $y=(1-\sqrt{2})x$
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2020
33.
Đường thẳng d song song \(\Delta\) nên nhận \(\left(3;-4\right)\) là 1 vtpt
\(\Rightarrow\) Nhận \(\left(4;3\right)\) là 1 vtcp
Phương trình tham số: \(\left\{{}\begin{matrix}x=4t\\y=3t\end{matrix}\right.\)
41.
\(\Delta_1\) nhận \(\left(2;-3m\right)\) là 1 vtpt
\(\Delta_2\) nhận \(\left(m;4\right)\) là 1 vtpt
Để 2 đường thẳng cắt nhau
\(\Leftrightarrow2.4\ne-3m^2\Leftrightarrow m^2\ne-\frac{8}{3}\) (luôn đúng)
Vậy hai đường thẳng cắt nhau với mọi m
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2020
21.
\(\overrightarrow{AB}=\left(-2;2\right)=-2\left(1;-1\right)\) nên pt đường thẳng AB:
\(1\left(x-1\right)+1\left(y-2\right)=0\Leftrightarrow x+y-3=0\)
\(\overrightarrow{CD}=\left(-5;0\right)=-5\left(1;0\right)\) nên pt CD có dạng:
\(0\left(x-2\right)+1\left(y-2\right)=0\Leftrightarrow y-2=0\)
Giao điểm 2 đường thẳng có tọa độ là nghiệm: \(\left\{{}\begin{matrix}x+y-3=0\\y-2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
31.
\(\Delta_1\) nhận \(\left(m+1;-1\right)\) là 1 vtcp
\(\Delta_2\) nhận \(\left(3;-4\right)\) là 1 vtpt
Để hai đường thẳng song song:
\(3\left(m+1\right)+4=0\Rightarrow m=-\frac{7}{3}\)
HK
28 tháng 4 2020
Bài 1:
\(\overrightarrow{u_{\Delta1}}=\left(2;-3\right)\Rightarrow\overrightarrow{n_{\Delta1}}=\left(3;2\right)\)
\(\Rightarrow\Delta_1:3\left(x-4\right)+2\left(y-1\right)=0\)
\(\Delta_1:3x+2y-14=0\)
\(\Rightarrow\Delta_1\equiv\Delta_2\)
Bài 6:
\(\frac{11}{12}\ne-\frac{12}{11}\Rightarrow\Delta_1\equiv\Delta_2\)
Bài 10:
\(\overrightarrow{AB}=\overrightarrow{u_{AB}}=\left(4;2\right)\)
CM
3 tháng 10 2019
Gọi M(x; y) là điểm thuộc đường phân giác tạo bởi 2 đường thẳng đã cho.
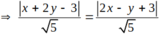
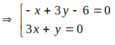
Chọn C.
HT
28 tháng 4 2021
\(y=x^3-3x^2+2x+2\Rightarrow y'=3x^2-6x+2\)
Vi \(\Delta\perp d:y=x-3\Rightarrow y'=-1\Leftrightarrow3x^2-6x+2=-1\)
\(\Rightarrow x=1\Rightarrow y=1-3+2+2=2\)
\(\Rightarrow\Delta:y=-1\left(x-1\right)+2\)
Gọi d là phân giác góc hợp bởi d1 và d2
Điểm N bất kì thuộc d có tọa độ \(N\left(x;y\right)\Rightarrow d\left(N;d_1\right)=d\left(N;d_2\right)\)
\(\Rightarrow\frac{\left|3x+4y+1\right|}{\sqrt{3^2+4^2}}=\frac{\left|x-2y+4\right|}{\sqrt{1^2+\left(-2\right)^2}}\)
\(\Leftrightarrow\left|3x+4y+1\right|=\sqrt{5}\left|x-2y+4\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+4y+1=\sqrt{5}x-2\sqrt{5}y+4\sqrt{5}\\3x+4y+1=-\sqrt{5}x+2\sqrt{5}y-4\sqrt{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(3-\sqrt{5}\right)x+\left(4+2\sqrt{5}\right)y+1-4\sqrt{5}=0\\\left(3+\sqrt{5}\right)x+\left(4-2\sqrt{5}\right)y+1+4\sqrt{5}=0\end{matrix}\right.\)